Quy Hoạch Động 2
Bài 9: Quy hoạch động 2
Trong bài này chúng ta xem xét 2 bài toán khác nhap áp dụng phương pháp quy hoạch động.
1. Khoảng cách sửa đổi
Ví dụ 1: Ta có thể sửa đổi FOOD và MONEY sử dụng 4 thao tác (trong số 3 thao tác cơ bản trên) như sau:
FOOD $\rightarrow$ MOOD $\rightarrow$ MOND $\rightarrow$ MONED $\rightarrow$ MONEY
Do đó khoảng cách sửa đổi giữa hai xâu này là không quá 4. Thực tế 4 cũng là khoảng cách sửa đổi giữa hai xâu này (chứng minh điều này có lẽ không dễ).
Bài toán tìm hiểu trong phần này của chúng ta là như sau:
Ta sẽ áp dụng phương pháp quy hoạch động vào bài toán này, và việc đầu tiên ta phải làm là xác định bài toán con. Một lựa chọn bài toán con khá tự nhiên đó là tính khoảng cách sửa đổi giữa hai chuỗi con $A[1,2,\ldots ,i]$ và $B[1,2,\ldots, j]$, kí hiệu là $D[i,j]$. Khi cần giải bài toán con này, ta có thể giả sử các bài toán con “nhỏ hơn” đã được giải (muốn biết tại sao thì bạn phải đọc bài trước.
Câu hỏi 1: bài toán như thế nào được gọi là “nhỏ hơn”?
Trả lời : Một cách xách định khá phổ biến, mà cụ thể trong trường hợp này, là bài toán có “tổng chỉ số” $i+j$ nhỏ hơn. Tức là bài toán tính khoảng cách sửa đổi giữa hai chuỗi con $A[1,2,\ldots ,i-1]$ và $B[1,2,\ldots, j]$, hoặc bài toán tính khoảng cách sửa đổi giữa hai chuỗi con $A[1,2,\ldots ,i]$ và $B[1,2,\ldots, j-1]$, đều là các bài toán nhỏ hơn theo tiêu chỉ tổngg chỉ số.
Trong một số bài toán khác đôi khi ta sử dụng tiêu chí như “cực đại của hai chỉ số”, tức là $\max(i,j)$. Nếu ta sử dụng tiêu chí này, nếu $j \geq i+2$, thì bài toán tính khoảng cách sửa đổi giữa hai chuỗi con $A[1,2,\ldots ,i+1]$ và $B[1,2,\ldots, j-1]$ được coi là bài toán nhỏ hơn.
Trong bài toán này, ta sẽ sử dụng tiêu chí tổng chỉ số làm tiêu chí cho bài toán nhỏ hơn. Điều đó có nghĩa là khi tìm giá trị $D[i,j]$, ta có thể giả sử các giá trị $D[i’,j’]$ với $i’+j’ < i+j$ đều đã sẵn có. Khi đó, ta có thể tìm lời giải cho bài toán con $D[i,j]$ như sau. Giả sử ta có hai xâu $A[1,2,\ldots ,i]$ và $B[1,2,\ldots, j]$. Ta có ba lựa chọn để áp dụng ba thao tác với cơ bản với $A[i]$:
- Xóa $A[i]$. Như vậy $D[i,j] = D[i-1,j]+1$. Lý do $+1$ là vì ta đã áp dụng xoá với $A[i]$.
- Chèn kí tự $B[j]$ vào sau $A[i]$. Khi đó $A[i+1] = B[j]$, và ta chỉ cần chuyển đổi $A[1,2\ldots, i]$ sang $B[1,\ldots, j-1]$. Như vậy $D[i,j] = D[i,j-1]+1$.
- Thay thế $A[i]$ bằng $B[j]$. Ta có hai trường hợp con ở đây: nếu $A[i] \not= B[j]$, khi đó $D[i,j] = D[i-1,j-1]+1$. Ngược lại ($A[i] = B[j]$), $D[i,j] = D[i-1,j-1]$
Câu hỏi 2: Tại sao ta không thực hiện xoá $B[j]$ và gọi lời giải bài toán con $D[i,j-1]$?
Trả lời: (gợi ý) xem lại định nghĩa của khoảng cách sửa đổi.
Trường hợp cơ sở của bài toán là khi $i = 0$ hoặc $j=0$; khi đó, khoảng cách tương ứng là $D[0,j] = j$ hoặc $D[i,0] = i$. Định nghĩa:
$[x\stackrel{?}{\not=}y]= \begin{cases} 1, & \mbox{if } x \not= y\\ 0, & \mbox{if } \mbox{otherwise} \end{cases}$
Giả mã của giải thuật quy hoạch động như sau:
1. for $i \leftarrow 0$ to $n$
2. $D[i,0] \leftarrow i$
3. for $j \leftarrow 0$ to $m$
4. $D[0,j] \leftarrow j$
5. for $i \leftarrow 1 $ to $n$
6. for $j \leftarrow 1 $ to $m$
7. $D[i,j] \leftarrow \min\{D[i-1,j] + 1, D[i,j-1]+1, D[i-1,j-1]+ $
$[A[i] \stackrel{?}{\not=}B[j]]\}$
8. return $D[n,m]$
Ví dụ 2: Xét $A[1,2] = ab$ và $B[1,2] = ca$. Theo khởi tạo $D[0,0] = 0, D[0,1] = D[1,0]=1, D[0,2] = D[2,0] = 2$. Theo cách ta cập nhật trong giải thuật, các giá trị lần lượt được cập nhật là $D[1,1] = 1$, $D[1,2] = 1$, $D[2,1] = 2$ và $D[2,2] = 2$. Như vậy khoảng cách giữa hai xâu này là $2$.
Thuật toán EditDistance chỉ đưa ra giá trị khoảng cách. Tuy nhiên, bạn có thể tìm ra cách sửa đổi $A$ thành $B$ sử dụng đúng $D[n,m]$ thao tác bằng phương pháp truy vết (xem bài tập 1).
Phân tích thời gian và bộ nhớ: Thời gian tính của thuật toán EditDistance bằng thời gian cần thiết để cập nhật mảng $D[1,2,\ldots,n][1,2,\ldots,m]$. Mỗi phần tử của mảng mất thời gian $O(1)$ để cập nhật. Do đó thời gian tính của thuật toán là $O(m\cdot n)$. Bộ nhớ của thuật toán cũng là $O(m\cdot n)$ để lưu bảng. Trong bài tập 2, ta sẽ tìm hiểu cách giảm bộ nhớ của thuật toán xuống còn $O(\min(n,m))$.
TÍnh đúng đắn của thuật toán: Không khó để thấy rằng đầu ra $D[n,m]$ sẽ cho ta biết số thao tác ta có thể áp dụng để chuyển $A$ thành $B$. Điều ta cần chứng minh là đầu ra $D[n,m]$ cũng là số thao tác ít nhất, và ta thực hiện điều này bằng quy nạp. Dễ thấy nếu $B[m] = A[n]$, thì ta chỉ cần đổi $A[1,\ldots, n-1]$ sang $B[1,\ldots, m-1]$ sử dụng $D[n-1,m-1]$ thao tác. Theo giả thiết quy nạp, đây cũng là số thao tác nhỏ nhất. Nếu $B[m]\not. = A[n]$, để chuyển đổi, xâu $A$ cuối cùng cũng phải kết thúc bằng $B[m]$. Ta chỉ có hai cách: hoặc là thay thế phần tử cuối cùng của $A$ bằng $B[m]$, hoặc chèn $B[m]$ vào cuối. Cả hai cách đều dần đến bài toán con nhỏ hơn và lúc đó ta có thể áp dụng giả thiết quy nạp. Phần còn lại của chứng minh chỉ mang tính thủ tục.
2. Subset Sum
Trong bài quay lui, chúng ta đã phát triển thuật toán với thời gian $2^n$ cho bài toán Subset Sum. Trong bài này ta phát triển thuật toán quy hoạc động giải bài toán này trong thời gian $O(Tn)$. Trước hết ta nhắc lại bài toán:
Nhắc lại ý tưởng ta đã học trong bài thuật toán quay lui. Xét một phần tử $x \in X$, tồn tại một dãy con có tổng bằng $T$ nếu một trong hai điều kiện sau là đúng:
- Tồn tại một tập con của $X \setminus \{x\}$ có tổng bằng $T - x$
- Tồn tại một tập con của $X \setminus \{x\}$ có tổng bằng $T$
Điều kiện đó gợi ý cho ta chọn bài toán con:
Xác định xem trong tập con có $i$ phần tử $X_i =\{X[1], X[2], \ldots, X[i]\}$ của $X$ có một tập con (của tập $X_i$) tổng bằng $t$ hay không?
Ta kí hiệu $S[i,t] = True$ nếu câu trả lời là có tồn tại và $False$ nếu ngược lại. Như vậy ta có công thức đệ quy:
$S[i,t] = \begin{cases} True, & \mbox{if } t = 0 \\ False, & \mbox{if } t < 0 \mbox{ or } i < 0 \\ S[i-1,t-X[i]]\vee S[i-1,t], & \mbox{otherwise } \end{cases}$
Dấu $\vee$ là phép toán logic OR. Biểu thức $S[i,t] = False$ khi $t < 0$ hoặc $i < 0$ có vẻ tầm thường (và thực sự là tầm thường), nhưng lại khá cần thiết khi lập trình để tránh gọi giá trị của mảng khi chỉ số âm. Giả mã của thuật toán như sau:
$S[0,0] \leftarrow $ True
for $t \leftarrow 1$ to $T$
$S[0,t] \leftarrow $ False
for $i \leftarrow 1$ to $n$
$S[i,0] = $ True
for $t \leftarrow 1$ to $X[i]-1$
$S[i,t] \leftarrow S[i-1,t]$ $\ll$avoid the case $t - X[i] < 0 \gg$
for $t \leftarrow X[i]$ to $T$
$S[i,t] \leftarrow S[i-1,t] \vee S[i-1,t-X[i]]$
return $S[n,T]$
Tính đúng đắn của thuật toán có thể chứng minh bằng phương pháp quy nạp. Chứng minh này coi như bài tập cho bạn đọc.
Phân tích thời gian và bộ nhớ: Thời gian tính toán của thuật toán SubsetSum có thể được quy về thời gian cập nhật các phần tử của mảng $S[n,T]$. Vì mỗi phần tử của mảng được cập nhật trong thời gian $O(1)$, thời gian tính toán của thuật toán là $O(nT)$. Ngoài ra, ta có thể thấy bộ nhớ của thuật toán sử dụng là $O(nT)$ để lưu mảng $S[n,T]$. Phần bộ nhớ khác không đáng kể so với số này.
3. Tham khảo
[1] Jeff Erickson, Dynamic Programming Lecture Notes , UIUC.
[2] Backurs, Arturs, and Piotr Indyk. “Edit Distance Cannot Be Computed in Strongly Subquadratic Time (unless SETH is false).” arXiv preprint arXiv:1412.0348 (2014).
[3] Sanjoy Dasgupta, Christos Papadimitriou, and Umesh Vazirani. Algorithms. 1st Edition). McGraw-Hill Higher Education, (2008).
4. Bài tập
Bài 1: Áp dụng kĩ thuật truy vết, in ra quá trình chuyển xâu $A$ thành xâu $B$ như ở trong ví dụ FOOD - MONEY sau khi thuật toán EditDistance đã hoàn thành.
Bài 2: Trong bài tập này, ta tìm hiểu cách cải thiện bộ nhớ của thuật toán EditDistance. Ý tưởng dựa trên nhận xét sau:
Phần tử mảng $D[i,j]$ chỉ phụ thuộc và 3 phần tử liền kề trong bảng như trong hình trái của hình dưới đây.
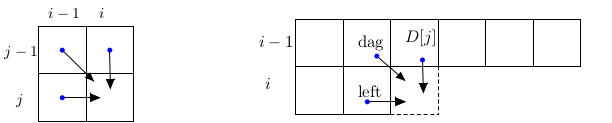
Dựa vào nhận xét này, cải tiến bộ nhớ của thuật toán EditDistance xuống còn $O(\min(n,m))$.
Bài 3: Áp dụng truy vết quy hoạch động, in ra tập các phần tử con của $X$ có tổng bằng $T$ trong bài toán Subset Sum.