Quy Hoạch Động I
Bài 8: Quy hoạch động I
Quy hoạch động (dynamic programming) về mặt nguyên lý khá giống với chia để trị: chia bài toán lớn thành các bài toán con, sử dụng lời giải của các bài toán con để tìm lời giải cho bài toán ban đầu. Điểm khác biệt lớn nhất so với chia để trị là, thay vì gọi đệ quy, quy hoạch động sẽ lưu lời giải của các bài toán con vào bảng (mảng một hoặc nhiều chiều), và sau đó lấy lời giải của bài toán con ở trong mảng đã tính trước để giải bài toán lớn. Việc lưu lại lời giải vào bộ nhớ khiến cho ta không phải tính lại lời giải của các bài toán con mỗi khi cần, do đó, tiết kiệm được thời gian tính toán. Tuy nhiên, ta phải thiết kế thuật toán theo hướng có thể sử dụng các chỉ số để mã hoá các bài toán con, và sử dụng các chỉ số đó làm chỉ số mảng để lưu trữ lời giải. Trong bài này ta xét ví dụ minh hoạ sau:
1. Dãy số Fibonacci
Bài toán dãy số Fibonacci như sau:
Dựa trực tiếp vào định nghĩa, ta có thể tính $F_n$ bằng phép đệ quy sau:
if $n$ < $2$
return $n$
else
return RecFib$(n-1)$ + RecFib$(n-2)$
Gọi $T(n)$ là số phép cộng phải thực hiện để tính $F_n$. Không khó để thấy $T(n)$ thoả mãn:
$T(n) = T(n-1) + T(n-2) + 1 \qquad T(0) = T(1) = 0 \qquad (2)$
Giải phương trình (2) ta được $T(n) = \Theta(\phi^n) $ với $\phi = (\sqrt{5} + 1)/2 \simeq 1.618$. Như vậy số phép cộng phải thực hiện để tính $F(n)$ theo phương pháp đệ quy là một hàm số mũ theo $n$. Câu hỏi đăt ra ở đây là liệu ta có thể tính $F(n)$ nhanh hơn không?
Để tìm câu trả lời, trước tiên ta hãy nghiên cứu sâu hơn thuật toán đệ quy thông qua cây đệ quy của thuật toán. Mỗi nút của cây là giá trị $F_n$ và nút con là các giá trị cần thiết tương ứng với hàm đệ quy của $F_n$. Các nút lá là $F_0$ hoặc $F_1$. Ví dụ cây đệ quy để tính $F_5$:
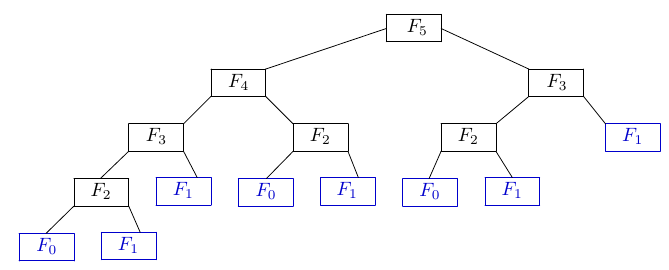Như vậy nhìn vào cây ta thấy để tính $F_5$, thủ tục đệ quy sẽ tính lại $F_2$ 3 lần và $F_3$ 2 lần.
Để tránh thực hiện các phép tính cùng một giá trị, ta sẽ sử dụng một mảng, mà ta đặt luôn tên là mảng $F[0,1,\ldots, n]$. Giá trị $F[i]$ của mảng sẽ lưu giá trị của hàm Fibonaaci $F(i)$ cần tính. Theo định nghĩa, ta có thể thiết lập $F[0] = F(0) = 0$ và $F[1] = F(1) = 0$.
Giá trị $F[i]$, với $i\geq 2$, sẽ được tính thế nào? Khi cần tính $F[i]$, ta hoàn toàn có thể giả sử các giá trị $F[0], F[1],\ldots, F[i-1]$ đã tính được trước đó. (Đây là một dạng giả sử kiểu quy nạp.) Như vậy theo định nghĩa của dãy Fibonacci, ta có thể tính:
$F[i]= F[i-1] + F[i-2] \qquad (3)$
Ghi chú 1: Trong phương trình (3), các giá trị $F[i-1]$ và $F[i-2]$ được lấy ra trực tiếp từ mảng $F$, chứ không phải là thủ tục gọi đệ quy.
Giá trị của hàm Fibonacci $F(n)$ chính là $F[n]$. Như vậy ta đã thiết kế xong giải thuật quy hoạch động cho bài toán toán 1. Khi thực thi thuật toán, ta phải chú ý thực thi sao cho, trước khi ta điền vào ô thứ $i$ của mảng $F$, tức là tính $F[i]$ theo phương trình (3), ta phải đảm bảo các giá trị $F[i-1], F[i-2]$ đã được tính trước đó. Ta có thể đảm bảo điều này bằng cách cập nhật theo vòng lặp. Chi tiết giả mã như sau:
$F[0] \leftarrow 0; F[1] \leftarrow 1$
for $i \leftarrow 2$ to $n$
$F[i] \leftarrow F[i-1] + F[i-2]$
return $F[n]$
Tính đúng đắn của thuật toán có thể chứng minh trực tiếp từ định nghĩa. Do thuật toán chỉ thực hiện một phép cộng trong mỗi vòng lặp for, tổng số phép cộng thực hiện là $n-1 = O(n)$. Thuật toán này nhanh hơn luỹ thừa lần thuật toán đệ quy theo định nghĩa.
Tổng kết: Đối chiếu lại với những gì đã nói đầu tiên, rõ ràng thuật toán quy hoạch động cho bài toán Fibonacci thực hiện lưu kết quả tính vào bảng $F[.]$, do đó, nó cải thiện được rất nhiều so với đệ quy. Tuy nhiên, cách mã hoá bài toán con của bài toán Fibonacci khá rõ ràng, mỗi bài toán con “tính số Fibonacci thứ $i$” được mã hoá bằng một chỉ số $i$. Do đó, ta có thể truy nhập lời giải của bài toán con chỉ bằng cách gọi $F[i]$. Thông thường các bài toán giải được một cách hiệu quả bằng phương pháp quy hoạch động, cách mã hoá bài toán con không đơn giản như vậy. Xét bài toán tiếp theo đây.
2. Dãy con tăng dài nhất
Bài toán dãy con tăng dài nhất (longest increasing subsequence-LIS) được phát biểu như sau.
Ví dụ 1: $A[10] = {1,6,5,4,7,8,2,9,0,10}$, (một trong số) dãy con tăng dài nhất là ${1,6,7,8,9,10}$ với chiều dài $6$.
Trước hết ta giải bài toán “dễ hơn” một chút: tìm chiều dài của dãy con tăng dài nhất của $A[1,2,\ldots,n]$. Như trong ví dụ, $6$ là số cần tìm vì dãy con tăng dài nhất chỉ có chiều dài $6$. Quá trình tìm chiều dài thông thường sẽ cho ta phương pháp tìm dãy con bằng cách truy vết.
Ghi chú 1: Đối với hầu hết các thuật toán quy hoạch động ta thường chỉ cần tìm một đặc tính đơn giản của lời giải như chiều dài hoặc chi phí, sau đó lời giải có thể tìm được thông qua truy vết.
Phân tích bài toán con: Bài toán con của ta xuất phát từ việc xét mảng con $A[1,2,\ldots, i]$. Giả sử ta giải bài toán gốc trên mảng con này, ta sẽ tìm chiều dài của dãy con tăng dài nhất của mảng $A[1,2,\ldots, i]$. Nếu ta đã tìm được chiều dài đó rồi, ví dụ $10$, làm thế nào ta có thể mở rộng lời giải cho mảng $A[1,2,\ldots, i+1]$? Có lẽ khó có thể mở rộng nếu định nghĩa bài toán con một cách trực tiếp như vậy.
Giả sử ngoài việc xác định được chiều dài của bài toán con, nếu ta (bằng cách nào đó) có thể lưu trữ được phần tử cuối cùng của dãy con tăng dài nhất, liệu ta có thể mở rộng ra lời giải cho mảng $A[1,2,\ldots, i+1]$ được không? Có lẽ cũng không, vì một dãy có thể có nhiều mảng con tăng khác nhau. Xét ví dụ dưới đây:
Ví dụ 2: Xét $n = 10$ và mảng $A[10] = {1,5,2,3,6,4,8,7,9,0,10}$, và $i =5$. Tức mảng con $A[1,2,\ldots, 5] = {1,5,2,3,6}$, và một mảng con tăng dài nhất là ${1,5,6}$. Do đó, nếu chỉ lưu phần tử cuối cùng của mảng con là $6$ (và chiều dài $3$) thì ta không mở rộng được lời giải cho mảng con $A[1,2,\ldots, 6]$ vì $A[6] < 6$. Tuy nhiên, $A[1,2,\ldots, 5]$ có một mảng con khác là ${1,2,3}$, cũng có chiều dài $3$, và nếu ta lưu phần tử cuối cùng $3$, thì ta có thể mở rộng ra tìm lời giải cho mảng con $A[1,2,\ldots, 6]$ thành ${1,2,3,4}$ vì $A[6] = 4 > 3$.
Ví dụ 2 cho ta một gợi ý về bài toán con: ngoài xác định chiều dài của bài toán con, nếu ta (bằng cách nào đó) có thể lưu trữ được mọi phần tử cuối cùng của tất cả các dãy con dài nhất có thể có, thì ta có thể mở rộng ra được lời giải cho mảng $A[1,2,\ldots, i+1]$ bằng cách so sánh $A[i+1]$ với từng phần tử kết thúc đó. Nếu $A[i+1]$ lớn hơn hoặc bằng bất kì phần tử kết thúc nào, thì dãy con tăng trong $A[1,2,\ldots, i+1]$ sẽ có chiều dài lớn hơn. Ngược lại, dãy con tăng dài nhất của $A[1,\ldots, i+1]$ và $A[1,\ldots, i]$ có cùng chiều dài.
Phân tích trên gợi ý cho ta cách “mã hoá” bài toán con như sau:
Gọi $L[i]$ với $i \geq j$ là chiều dài của dãy con tăng dài nhất của $A[1,2,\ldots,i]$ kết thúc bằng $A[i]$.
Ban đầu, ta khởi tạo mảng $L[i] = 1$ với mọi $i, 1\leq i \leq n$. (Lý do ta khởi tạo $1$ là vì $A[1,2,\ldots, i]$ luôn có một dãy con có chiều dài $1$ [chỉ bao gồm $A[i]$] kết thúc tại $A[i]$.) Nên nhớ rằng khi ta tìm lời giải của $A[1,2,\ldots, i+1]$, ta có thể giả sử lởi giải của $A[1,\ldots, j]$ với mọi $j < i+1$ đều đã sẵn có trong bảng $L$.
Ví dụ 3: Xét $n = 10$ và mảng $A[10] = {1,5,2,3,6,4,8,7,9,0,10}$, và $i =5$. Ta sẽ có $L[1] = 1, L[2] = 2, L[3] = 2, L[4] = 3, L[5] = 6$. Câu hỏi đặt ra cho bạn: $L[6]$ có giá trị bao nhiêu?
Theo định nghĩa, $L[i+1]$ chính là chiều dài của dãy con tăng dài nhất của $A[1,2,\ldots, i+1]$ kết thúc tại $A[i+1]$. Điều đó có nghĩa là trong dãy con tăng đó, $A[i+1]$ là lớn nhất. Do đó, ta chỉ cần tìm một chỉ số $j < i+1$ sao cho (1) $A[j] \leq A[i+1]$ và (2) $L[j]$ có giá trị lớn nhất trong số các chỉ số $j$ thoả mãn (1). Khi đó, theo định nghĩa, $L[i+1] = L[j] + 1$ vì $A[i+1] \geq A[j]$.
Câu hỏi: giả sử ta đã điền được toàn bộ mảng $L[1,2\ldots, n]$, lời giải của bài toán của ta là gì?
Trả lời: chiều dài của dãy con tăng dài nhất, theo định nghĩa của mảng $L$, là $\max_{1\leq i\leq n}L[i]$.
Để tránh phải duyệt qua toàn bộ mảng $L$ để tìm lời giải, ta áp dụng một mẹo nhỏ: thêm phần tử $A[n+1]$ có giá trị cực lớn, đảm bảo lớn hơn mọi phần tử của mảng $A$. Như vậy mảng con tăng dài nhất sẽ luôn kết thúc tại $A[n+1]$. Chi tiết giả mã như sau:
1. for $i \leftarrow 1$ to $n+1$
2. $L[i] \leftarrow 1$
3. $A[n+1] \leftarrow \infty$
4. for $i \leftarrow 2$ to $n+1$
5. for $j \leftarrow 1$ to $i-1$
6. if $A[i] \geq A[j]$
7. $L[i]\leftarrow \max(L[i], L[j] + 1)$
8. return $L[n+1]-1$
Tính đúng đắn của thuật toán: Điểm đáng chú ý duy nhất của thuật toán là dòng 6 và 7. Giá trị của $L[i]$ chỉ thay đổi khi $L[i] \geq A[j]$ và chỉ số $j$ hiện tại có giá trị $L[j]$ lớn nhất trong số tất cả các chỉ thuộc tập ${1,2,\ldots, j}$. Phần còn lại của tính đúng đắn của thuật toán có thể chứng minh bằng quy nạp, dựa trên định nghĩa của mảng $L$ và nhữn gì ta đã thảo luận ở trên.
Thời gian tính toán: Ta thực hiện hai vòng lặp lồng nhau ở dòng 4 và 5. Tổng số lần lặp là $\sum_{i=2}^{n+1} \sum_{j=1}^{i-1} 1 = \Theta(n^2)$. Do mỗi vòng lặp ta chỉ thực hiện một hằng số phép toán cơ bản, do đó, thời gian tính toán của thuật toán là $O(n^2)$.
Truy vết lời giải: Ta dựa vào mảng $L[1,2,\ldots, n]$ để truy vết tìm dãy con tăng dài nhất. Ý tưởng cơ bản như sau: giả sử ta có chiều dài của dãy con tăng dài nhất là $M$ (đã tính được bởi thuật toán ở trên). Vì $L[i]$ là chiều dài của dãy con tăng lớn nhất của mảng $A[1,2,\ldots, i]$ kết thúc bởi $A[i]$, chỉ số $i$ lớn nhất sao cho $L[i] = M$ chính là chỉ số của phần tử cuối cùng của mảng con tăng lớn nhất của $A[1,2,\ldots, n]$.
Giả mã của thuật toán truy vết như sau:
$m \leftarrow +\infty$
for $i \leftarrow n$ to $1$
if $L[i] = M$ and $A[i] \leq m$
print $A[i]$
$m \leftarrow A[i]$
$M \leftarrow M -1$
Dễ thấy thời gian để tìm các phần tử của mảng con tăng là $O(n)$. Tính đúng đắn của thuật toán coi như bài tập cho bạn đọc.
Lời cám ơn: Cám ơn bạn Xuan Tu đã đưa ra cách đơn giản hoá giả mã của thuật toán LongestIncreasingSubsequence trong phiên bản trước đây của bài viết.
3. Tham khảo
[1] Jeff Erickson, Dynamic Programming Lecture Notes , UIUC.
[2] Sanjoy Dasgupta, Christos Papadimitriou, and Umesh Vazirani. Algorithms. 1st Edition). McGraw-Hill Higher Education, (2008).
[3] http://stackoverflow.com/questions/6129682/longest-increasing-subsequenceonlogn