Cây Khung Nhỏ Nhất
Bài 11: Cây khung nhỏ nhất
Trong bài này, chúng ta tìm hiểu bài toán tìm cây khung nhỏ nhất (minimum spanning tree) của một đồ thị đơn, vô hướng và liên thông. Đây là một bài toán điển hình trên đồ thị, có rất nhiều ứng dụng thực tiễn trong thiết kế mạng.
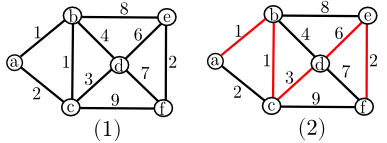
Ví dụ 1: Đồ thị (hình (1)) với trọng số và một cây khung nhỏ nhất (hình (2)) với trọng số 13.
Ta sẽ tìm hiểu một số tính chất cơ bản của cây khung mà ta có thể sử dụng trong thuật toán tìm cây khung nhỏ nhất.
1. Một số tính chất của cây khung
Một số tính chất chung của một cây khung (không nhất thiết là nhỏ nhất):
- $T$ có đúng $n-1$ cạnh.
- Với mỗi cặp đỉnh $u,v$, tồn tại một và chỉ một đường đi nối hai đỉnh $u,v$ trong $T$.
- Thêm bất kì một cạnh nào vào $T$ sẽ tạo ra một (và chỉ một) chu trình.
Chứng minh các tính chất trên không khó, và ta sẽ coi như bài tập cho bạn đọc.
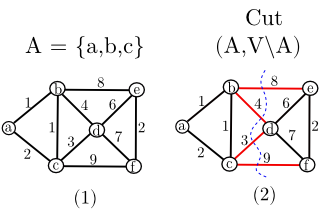
Ví dụ 2: Lát cắt tương ứng với ${(a,b,c)}$ của đồ thị trong hình (a) là các cạnh màu đỏ trong hình (b).
Một số tính chất sau của cây khung nhỏ nhất sẽ rất hữu ích trong thiết kế thuật toán.
- Tính Chu Trình (Cycle Property): Cạnh có trọng số lớn hơn các cạnh khác trong cùng một chu trình (nào đó) của đồ thị không nằm trong bất kì cây khung nhỏ nhất nào.
- Tính Cắt (Cut Property): Cạnh có trọng số nhỏ hơn các cạnh khác trong cùng một lát cắt (nào đó) của đồ thị $G$ nằm trong mọi cây khung nhỏ nhất.
- Nếu có duy nhất một cạnh có trọng số nhỏ nhất thì bất kì cây khung nhỏ nhất nào cũng phải chứa cạnh này.
Phương pháp chứng minh các tính chất trên đều giống nhau, sử dụng phương pháp lập luận tráo đổi (exchange argument). Ta sẽ chứng minh tính chất (4) và (5) để minh họa cho phương pháp chứng minh này. Chứng minh (6) dễ hơn (4) và (5); chi tiết coi như bài tập cho bạn đọc.
Chứng minh: (4) Giả sử cạnh $e$ lớn hơn các cạnh khác trong cùng một chu trình $C$ và giả sử một cây khung nhỏ nhất $T$ chứa $e$. Xóa $e$ khỏi $T$, ta sẽ thu được hai cây $F_1,F_2$. Do $C$ là một chu trình, tồn tại một cạnh khác $e$, gọi là $f$, của $T$ nối $F_1$ với $F_2$. Do đó $T\cup {(f)} - {(e)}$ là một cây khung của $G$ có trọng số nhỏ hơn $T$ (vì $w(f) < w(e)$), trái với giả thiết $T$ là một cây khung nhỏ nhất.
(5) Giả sử cạnh $e$ nhỏ hơn các cạnh khác trong cùng một lát cắt $L$ và giả sử tồn tại một cây khung nhỏ nhất $T$ không chứa $e$. Thêm $e$ vào $T$, ta sẽ thu được một chu trình $C$ chứa $e$. Do $L$ là lát cắt, $C$ phải chứa ít nhất một cạnh $f\not= e$ của $L$. Do đó, $T\cup {(e)} - {(f)}$ là một cây khung của $G$ có trọng số nhỏ hơn $T$ (do $w(e) > w(f)$), trái với giả thiết $T$ là một cây khung nhỏ nhất. $\blacksquare$
2. Thuật toán Kruskal
Thuật toán Kruskal là một thuật toán kiểu tham lam, cực kì đơn giản và có thể mô tả bằn một câu:
Ta sẽ cắt nghĩa từ nếu có thể ở trên. Tưởng tượng ta sẽ duy trì một tập cạnh $T \subseteq E$, ban đầu khởi tạo rỗng. Khi thuật toán kết thúc, $T$ sẽ là một cây khung (nhỏ nhất) của $G$. Tại mỗi bước, ta sẽ xét một cạnh $e$, nếu $T\cup e$ không có chu trình thì $e$ sẽ được gọi là cạnh có thể thêm vào $T$. Theo mô tả ở , các cạnh ta xét sẽ theo thứ tự tăng dần của trọng số, vì ta muốn đưa nhiều cạnh có trọng số nhỏ vào $T$ và hi vọng các cạnh này tạo thành một cây khung nhỏ nhất. Giả mã của thuật toán Kruskal như sau:
1. $T \leftarrow (V, \emptyset)$ $\ll $ there is no edge in $T \gg$
2. sort edges in $E$ in $\uparrow$ order of weight
3. let $e_1,\ldots, e_m$ be edges in the sorted ofder.
4. for $i \leftarrow 1$ to $m$
5. if $T\cup {(e_i)}$ has no cycle
6. $T\leftarrow T\cup {(e_i)}$
7. return $T$.
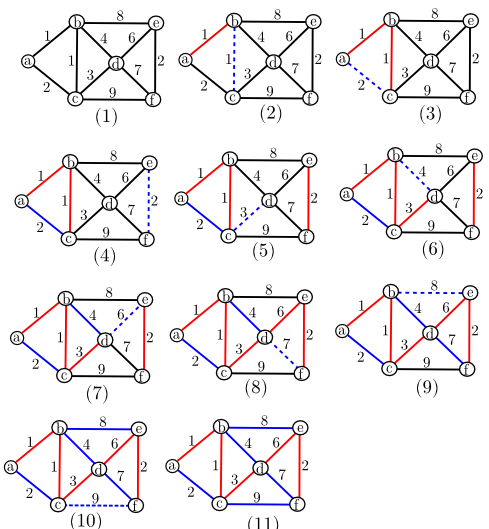
Ví dụ 3: Hình sau minh hoạ các bước chạy của thuật toán Kruskal với đồ thị trong ví dụ 1. Các cạnh màu đỏ là các cạnh nằm trong cây khung nhỏ nhất. Các cạnh màu xanh là các cạnh đã được xét và không nằm trong cây khung. Các cạnh màu xanh gạch ngang là cạnh sẽ được xem xét đưa vào cây khung trong bước tiếp theo. Thứ tự các cạnh được xét là theo chiều tăng dần của trọng số.
Tất cả các bước của thuật toán Kruskal đều không khó thực thi, ngoại trừ bước số 6. Để kiểm tra một đồ thị (vô hướng, có thể không liên thông) có chu trình hay không, ta chỉ cần thực hiện các thuật toán duyệt đồ thị (BFS và DFS đều được). Trong trường hợp này, phép duyệt có thể thực hiện trong thời gian $O(n)$, chứ không phải $O(n+m)$, và do đó thuật toán Kruskal có thể thực hiện được trong thời gian $O(mn)$. Tạm gác vấn đề thực thi qua một bện; ta sẽ tìm hiểu sâu hơn ở dưới và trong phần bài tập. Ta tập trung vào câu hỏi: tại sao đầu ra của thuật toán Kruskal là một cây khung nhỏ nhất?
2.1. Tính đúng đắn của thuật toán Kruskal
Ta phải chứng minh hai điều: (a) đầu ra của thuật toán là một cây khung và (b) cây đó có trọng số nhỏ nhất trong số tất cả các cây khung của đồ thị.
Ta sẽ chứng minh (a) trước. Đầu tiên, ta dễ thấy đầu ra $T$ không có chu trình vì dòng 5 của thuật toán sẽ đảm bảo điều này. Như vậy, $T$ sẽ là cây nếu liên thông (chỉ có duy nhất một thành phần liên thông). Giả sử đầu ra không liên thông, $T$ sẽ có ít nhât hai thành phần liên thông (mỗi thành phần liên thông có thể chỉ là 1 đỉnh). Chọn hai thành phần liên thông $F_1,F_2$ của $T$, sao cho tồn tại một cạnh của $G$ nối hai thành phần này. Ta luôn chọn được vì $G$ liên thông. Gọi $e_k$ là cạnh có trọng số nhỏ nhất nối $F_1,F_2$. Cạnh $e_k$ này không thuộc $T$ vì nếu không $F_1,F_2$ sẽ là chỉ là một thành phần mà thôi. Nhưng khi kiểm tra điều kiện ở dòng màu đỏ, $T\cup {(e_k)}$ rõ ràng không có chu trình. Điều đó có nghĩa ta sẽ thêm $e_k$ vào trong $T$ ngay sau đó. Điều này trái với giả sử $e_k$ không thuộc $T$. Do đó $T$ phải liên thông, i.e, $T$ là một cây.
Giờ ta sẽ chứng minh (b). Do thuật toán Krukal là một thuật toán tham lam, ta sẽ dùng phép biện luận tráo đổi như đã áp dụng trong bài thuật toán tham lam. Gọi $F$ là một cây khung nhỏ nhất của $G$ sao cho số cạnh chung giữa $F$ và $T$ là lớn nhất. Nếu $F = T$ thì rõ ràng $T$ là một cây khung nhỏ nhất. Do đó, giả sử $F \not= T$.
Gọi $T = {(t_1,t_2, \ldots, t_{n-1})}$ và $F = {(f_1,f_2,\ldots,f_{n-1})}$ lần lượt là thứ tự các cạnh của $T$ và $F$ sắp xếp theo chiều tăng của trọng số. Gọi $i$ là chỉ số nhỏ nhất sao cho cạnh $t_i$ và cạnh $f_i$ là hai cạnh khác nhau. Theo cách chọn $i$, ta suy ra $i \leq n-2$ và $f_k = t_k, 1 \leq k \leq i-1$. Do đó, ${(t_1,\ldots, t_{i-1})} \cup {(f_i)}$ không có chu trình.
Ta sẽ có $w(t_i) \leq w(f_i)$, vì nếu không, dòng màu đỏ trong thuật toán sẽ kiểm tra cạnh $f_i$ trước khi kiểm tra cạnh $t_i$, và do ${(t_1,\ldots, t_{i-1})} \cup {(f_i)}$ không có chu trình, $f_i$ sẽ được thêm vào $T$ trước $t_i$. Hay nói cách khác, $f_i$ chính là cạnh thứ $i$ của $T$; trái với giả thiết $f_i \not= t_i$.
Xét đồ thị $H = F \cup {(t_i)}$. $H$ sẽ có một chu trình $C$. Chu trình $C$ có hai tính chất sau:
- $C$ chứa $t_i$. Nếu không, $C$ sẽ là một chu trình của $F$, trái với giả thiết $F$ là một cây.
- $C$ chứa ít nhất một cạnh $f_j$ sao cho $j \geq i $. Nếu không, $C$ là tập con của ${(f_1,\ldots,f_{i-1})} \cup {t_i}$; tập này cũng chính là tập ${(t_1,\ldots, t_i)}$. Hay nói cách khác $C$ là tập con của $T$, trái với tính chất $T$ là một cây.
Gọi $F’ = H - {(f_j)}$; $F’$ là một cây (tại sao?). Do $w(f_j) \geq w(f_i) \geq w(t_i)$, $w(F’) \leq w(F)$. Từ đó suy ra $F’$ cũng là một cây khung nhỏ nhất. Nhưng rõ ràng $F’$ có số cạnh chung với $T$ nhiều hơn $F$. Điều này trái với giả thiết $F$ là cây khung nhỏ nhất có số cạnh chung nhiều nhất với $T$. Như vậy, $F = T$, i.e, $T$ là cây khung nhỏ nhất.
2.2. Thực thi thuật toán Kruskal
Như đã chỉ ra ở trên, ta chỉ cần thực hiện dòng 5 của thuật toán Kruskal một cách hiệu quả. Phép duyệt đồ thị cho ta thuật toán với thời gian $O(n)$ để thực hiện dòng này. Phần này ta đưa ra một cách nhìn khác, cho phép ta thực thi nó hiệu quả hơn.
Ta nhận xét thấy trong mỗi bước trung gian, $T$ là một rừng, i.e, mỗi thành phần liên thông của $T$ là một cây. Phép kiểm tra xem $T\cup {(e)}$ có chu trình hay không tương đương với kiểm tra xem hai đầu mút, gọi là $u,v$, của $e$ có thuộc cùng một cây trong rừng $T$ hay không.
- Nếu $u,v$ thuộc cùng một cây, $T\cup {(e)}$ sẽ có chu trình.
- Ngược lại, $T\cup {(e)}$ không có chu trình, và phép thêm $e$ vào $T$ sẽ tương đương với gộp 2 cây con của $T$ thành một cây mới bằng cạnh $e$.
Ta có thể biểu diễn mỗi cây của $T$ bằng một tập hợp: các đỉnh thuộc cùng một cây khi và chỉ khí nó nằm trong cùng một tập. Giả sử mỗi tập có một ID duy nhất để định danh tập hợp đó; hai tập khác nhau có ID khác nhau. Hai thao tác ta cần để thực hiện thuật toán Kruskal là:
- Find($x$): Trả lại id của tập hợp chứa $x$.
- Union($x,y$): Thay thế hai tập hợp $A,B$ lần lượt chứa $x$ và $y$ bằng tập hợp $A \cup B$. Ở đây ta giả sử phép Union luôn gộp 2 phần tử thuộc hai tập khác nhau.
Ngoài ra, ta còn thêm thao tác MakeSet($x$) để tạo tập hợp chỉ chứa một phần tử ${(x)}$. Khi đó thuật toán Kruskal có thể được thực hiện như sau:
1. $T \leftarrow (V, \emptyset)$ $\ll $ there is no edge in $T \gg$
2. for each $v \in V$
3. MakeSet($v$)
4. sort edges in $E$ in $\uparrow$ order of weight
5. let $e_1,\ldots, e_m$ be edges after sorting
6. for $i \leftarrow 1$ to $m$
7. let $u,v$ be two endpoints of $e_i$
8. if Find$(u) \not= $ Find($v$)
9. $T\leftarrow T\cup {(e_i)}$
10. Union$(u,v)$
11. return $T$.
Nhắc lại cấu trúc tập hợp: Trong bài viết này, mình giả sử bạn đọc đã làm quen với cấu trúc biểu diễn tập hợp sao cho thao tác trong dòng 8 và 10 thực hiện được trong thời gian $O(\log n)$ (thay vì $O(n)$ như phép duyệt đồ thị.) Ở đây mình chỉ nhắc lại cách thực thi các thao tác, chi tiết phân tích xem trong phần bài tập.
Ta sẽ dùng cấu trúc cây để biểu diễn một tập hợp. Mảng $P[1,\ldots,n]$ sẽ biểu diễn cấu trúc cây này. Nói cách khác, $P[v] = u$ nếu như $u$ là nút cha của $v$ trong cây (biểu diễn tập hợp chứa $u$ và $v$). Do đó, để kiểm tra xem hai phần tử $u,v$ có trong cùng một cây hay không, ta chỉ việc tìm xem nút gốc của cây biểu diễn có trùng nhau hay không. Gốc của cây cũng chính là ID của tập hợp.
Để phép tìm kiếm gốc của cây được thực hiện trong thời gian $O(\log n)$, ta sẽ muốn biểu diễn tập hợp đó bằng một cây sao cho đường đi từ một nút bất kì đến gốc có độ dài không quá $O(\log n)$. Nói cách khác, ta muốn các cây này có độ sâu không quá $O(\log n)$. Ban đầu mỗi tập chỉ là $1$ phần tử (dòng 3). Kích thước tập hợp tăng lên do ta thực hiện phép hợp (Union) ở dòng 10. Khi hợp hai tập hợp $A$ và $B$ có gốc là $a,b$. Ta có hai lựa chọ: (1) cho $a$ làm cha của $b$ bằng cách thiết lập $P[b] \leftarrow a$ (và do đó nó sẽ là gốc của tập hợp mới $A\cup B$.), hoặc ngược lại, (2) cho $b$ làm cha của $a$ bằng cách thiết lập $P[a] \leftarrow b$. Nếu ta thực hiện một cách tuỳ tiện (1) hoặc (2), chiều sâu của cây có thể rất lớn, như chỉ ra trong ví dụ sau:
Ví dụ 4: Xét các tập $(v_1), (v_2), \ldots,(v_n)$ được gộp theo thứ tự: $(v_1)$ gộp với $(v_2)$ thành $(v_1,v_2)$; sau đó $(v_1,v_2)$ được gộp với $(v_3)$ thành $(v_1,v_2,v_3)$; $\ldots$; cuối cùng $(v_1,\ldots, v_{n-1})$ được gộp với $(v_n)$ để tạo thành $(v_1,v_2,\ldots, v_n)$. Nếu tại bước thứ $i$, ta để $v_{i+1}$ làm gốc của tập $(v_1,v_2,\ldots, v_{i+1})$ thì cây cuối cùng sẽ là một đường đi $v_1 \rightarrow v_2 \rightarrow \ldots \rightarrow v_n$ gốc tại $v_n$; nói cách khác, nó có độ sâu $n-1$. Đây không phải là điều ta muốn.
Ví dụ 4 cho ta một ý tưởng chọn gốc: khi gộp tập $A,B$ tương ứng với gốc tại $a,b$, ta sẽ để nút biểu diễn tập có kích thước lớn hơn làm gốc của tập mới; nếu hai tập có kích thước bằng nhau thì chọn tuỳ ý một trong hai nút. Áp dụng cho ví dụ 4, ta sẽ thấy cây thu được có độ sâu $1$; nhỏ hơn nhiều so với độ sâu mong muốn $O(\log n)$.
Để thực hiện gộp theo kích thước, ta sẽ lưu trữ ở gốc $u$ của mỗi cây một biến $S[u]$ lưu trữ kích thước của cây. Giả mã của các thao tác biểu diễn tập hợp của ta sẽ như sau:
$P[x] \leftarrow x$
$S[x] \leftarrow 1$
if $P[x] \not= x$
$P[x] \leftarrow $ Find($P[x]$)
return $P[x]$
$\bar{x} \leftarrow $ Find($x$) $\ll$the root of $A\gg$
$\bar{y}\leftarrow $ Find($y$) $\ll$the root of $B\gg $
if $S[\bar{x}]> S[\bar{y}]$
$P[\bar{y}] \leftarrow \bar{x}$
$S[\bar{x}] \leftarrow S[\bar{x}] + S[\bar{y}] $
else
$P[\bar{x}] \leftarrow \bar{y}$
$S[\bar{y}] \leftarrow S[\bar{x}] + S[\bar{y}] $
Ta có tính chất sau; chứng minh xem trong phần bài tập.
Phân tích thời gian thuật toán Kruskal: Sắp xếp các cạnh của đồ thị theo trọng số mất thời gian $O(m\log m) = O(m \log n)$ (dùng merge sort chẳng hạn). Theo tính chất 1, mỗi thao tác Find($x$) và Union($x,y$) có độ phức tạp không quá $O(\log n)$. Do đó, vòng lặp trong dòng 6-11 có thể thực hiện trong thời gian $m \log n$. Vậy tổng thời gian của thuật toán là $O(m\log n)$. $\blacksquare$
3. Thuật toán Prim
Thuật toán Prim [5] tìm cây khung nhỏ nhất dựa trên tính cắt (tính chất 5) của cây khung. Thuật toán duy trì một tập đỉnh $A$ và một cây khung $T$ cho tập đỉnh này. Ban đầu, $A$ chỉ có một đỉnh (bất kì) của đồ thị và $T$ không chứa cạnh nào. Mỗi bước, thuật toán tìm ra đỉnh $u$ không thuộc $A$ sao cho cạnh kề với $u$ là cạnh có trọng số nhỏ nhất trong số các cạnh trong lắt cắt $(A,V\setminus A)$ và thêm $u$ vào $A$. Trong giả mã dưới đây, ta sử dụng $T$ để biểu diễn cả tập $A$ và cây khung của tập $A$ này. Cụ thể, lát cắt $(T,V\setminus T)$ sẽ là lát cắt tương ứng với các đỉnh trong $T$.
1. pick any vertex $u$
2. $T\leftarrow {(u )}$
3. while $T \not= V$ $\ll T$ does not contain all vertices$\gg$
4. $e \leftarrow$ the smallest edge of the cut $(T,V\setminus T)$
5. $T \leftarrow T \cup {(e)}$
6. return $T$
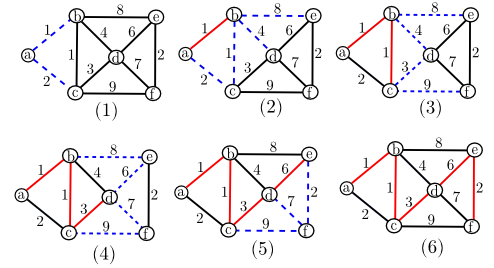
Ví dụ 5: Hình dưới đây minh hoạ các bước thực hiện thuật toán Prim. Các cạnh màu đỏ là các cạnh mà ta đã thêm vào cây khung nhỏ nhất. Các cạnh màu xanh gạch ngang là các cạnh của lát cắt mà ta xét để tìm ra cạnh cần thêm vào cây khung.
3.1. Tính đúng đắn của thuật toán Prim
Không khó để thấy rằng đầu ra của thuật toán Prim là một cây, vì ta không bao giờ đưa vào $T$ một cạnh giữa hai đỉnh đã thuộc $T$, theo định nghĩa của lát cắt. Do đó, ta chỉ còn cần chứng minh đầu ra là một cây khung nhỏ nhất.
Nếu mọi cạnh của đồ thị đều đôi một khác nhau, ta luôn đưa vào $T$ cạnh nhỏ nhất của một lát cắt, mà cụ thể là lát cắt ở dòng 4. Do đó, theo tính chất 5, $T$ phải là một cây khung nhỏ nhất (và cũng là duy nhất).
Trường hợp tồn tại các cạnh có cùng trọng số, để chứng minh tính đúng đắn của thuật toán Prim, ta cần chứng minh bổ đề sau:
Chứng minh: Thật vậy, gọi $F$ là một cây khung nhỏ nhất nhất không chứa $e$. Ta có $F\cup {(e)}$ sẽ chứa một chu trình $C$. Chu trình này phải chứ $e$. Do đó, $|C \cap (A, V\setminus A)| \not= \emptyset$. Do $C$ là một chu trình, nó sẽ chứa một số chẵn cạnh của lát cắt $(A, V\setminus A)$; nói cách khác, tồn tại một cạnh $f$ khác $e$ nằm trong cắt $(A, V\setminus A)$. Thêm nữa, $w(f)\geq w(e)$, do $e$ là cạnh có trọng số nhỏ nhất.
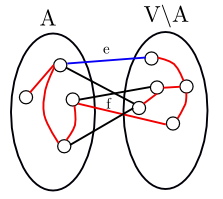
Gọi $T = F\cup {(e)} \setminus {(f)}$. $T$ là một cây khung của đồ thị và do $w(e) \leq w(f)$, ta suy ra $w(T) \leq w(F)$. Do đó, $T$ cũng phải là một cây khung nhỏ nhất vì $F$ là cây khung nhỏ nhất. Như vậy, $T$ là một cây khung nhỏ nhất chứa $e$. $\blacksquare$
Theo bổ đề $1$, đầu ra của thuật toán Prim cũng phải là cây khung nhỏ nhất mỗi cạnh của nó là một cạnh có trọng số nhỏ nhất của một lát cắt nào đó. $\blacksquare$
3.2. Thực thi thuật toán Prim
Gọi $n,m$ lần lượt là số đỉnh và số cạnh của đồ thị. Ta thấy thời gian thực thi thuật toán là $O(nF(n,m))$ trong đó $F(n,m)$ là thời gian để thực thi dòng màu đỏ vì sau mỗi vòng lặp, số đỉnh của $T$ tăng lên $1$. Cách thực thi dòng màu đỏ đơn giản nhất đó là duyệt qua tất cả các cạnh của lát cắt và tìm cạnh có trọng số nhỏ nhất. Thời gian của cách thực thi này có thể lên tới $O(m)$, và như vậy, tổng thời gian của thuật toán là $O(nm)$. Với đồ thị dầy ($m = O(n^2)$), cách này cho chúng ta thuật toán $O(n^3)$.
Ta sẽ tìm hiểu một cách thực thi hiệu quả hơn, có thời gian $O(n^2)$. Ta sẽ sử dụng biểu diễn là ma trận kề. Mỗi đỉnh $u$ không thuộc cây hiện tại $T$ ($u \in V\setminus T$), ta sẽ lưu một nhãn $d[u]$. Nhãn $d[u]$ là trọng số của cạnh nhỏ nhất trong số các cạnh từ $u$ tới các đỉnh trong $T$ hiện tại. Ta cũng lưu thêm một nhãn $M[u]$, trong đó $M[u] = v$ nếu $v\in T$ và $w(u,v) = d[u]$.
Để tìm cạnh nhỏ nhất của lát cắt (thực hiện dòng màu đỏ), ta sẽ duyệt qua tất cả các đỉnh trong $ V\setminus T$, tìm ra đỉnh $u$ có $d[u]$ nhỏ nhất. Khi đó, cạnh $(u,M[u])$ chính là cạnh nhỏ nhất của lát cắt $(T, V\setminus T)$. Do đó, ta có thể thực hiện dòng màu đỏ với $F(n,m) = O(n)$. Liệu chúng ta đã xong?
Còn một vấn đề nữa, đó là sau khi thêm một cạnh vào trong cây khung hiện tại $T$, ta phải cập nhật lại nhãn cho các đỉnh còn lại. Giả sử cạnh $(u,v)$, với $v = M[u]$, sẽ được thêm vào cây khung. Giả sử trước khi thêm cạnh này, $u \not\in T$. Để cập nhật nhãn, ta duyệt qua các đỉnh còn lại trong $V\setminus T$ và với mỗi đỉnh $x$, ta so sánh trọng số $w(u,x)$ với $d[x]$. Nếu $w(u,x)< d[x]$, ta sẽ cập nhật $d[x] = w(u,x)$ và $M[x] = u$. Nếu không ta sẽ giữ nguyên trọng số. Thao tác cập nhật này có thể thực hiện trong thời gian $O(n)$, do đó, tổng thời gian của thuật toán sẽ là $O(n^2)$.
pick any vertex $u$
$M[1,\ldots, n] \leftarrow {(0,\ldots,0)}$
$d[1, \ldots,n] \leftarrow {(\infty, \ldots, \infty)}$
for each neighbor $x$ of $u$
$M[x] \leftarrow u$
$d[x] \leftarrow w(u,x)$
$T \leftarrow \emptyset$
while $T \not= V$ $\ll T$ does not contain all vertices$\gg$
$u \leftarrow$ FindSmallestVertex$(d[1,\ldots,V], T)$
for each neighbor $x$ of $u$
if $x \not\in T$ and $w(u,x)$ < $d[x]$
$M[x] \leftarrow u$
$d[x] \leftarrow w(u,x)$
$T \leftarrow T \cup {((u,M[u]))}$ $\ll $ add edge $(u,M[u])$ to $ T\gg$
return $T$
$min \leftarrow +\infty, u \leftarrow 0$
for each $v \in V$
if $d[v]$ < $min$ and $v \not\in T$
$min \leftarrow d[v], u \leftarrow v$
return $u$
Khi giả mã trên, ta có thể nhận thấy từ mảng $M$, ta có thể xây dựng lại được cây $T$. Với mỗi $x$ mà $M[x] \not= 0$, $(x,M[x])$ chính là cạnh của cây $T$. Ta sẽ dùng thêm một mảng $inT[1,\ldots,n]$ trong đó $inT[u] = $ True nếu $u$ ở trong cây hiện tại và $inT[u] = $ False nếu ngược lại.
Ghi chú 1: Thực thi thuật toán Prim ở phần này chỉ phù hợp với đồ thị dầy với $\Omega(n^2)$ cạnh. Ta có thể thực thi thuật toán Prim với thời gian $O(m\log n)$ sử dụng cấu trúc Heap, như chi tiết sẽ phức tạp hơn thuật toán Kruskal.
Ghi chú 2: Với đồ thị dầy, ta nên sử dụng thuật toán $O(n^2)$ của Prim, vì thực thi đơn giản mà thời gian chạy lại tối ưu. Với đồ thị thưa, ta nên sử dụng thuật toán Kruskal.
Ghi chú 3: Thuật toán Prim, theo Wikipedia, được tìm ra đầu tiên bởi Jarník [2] năm 1930, sau đó được Prim [5] độc lập phát triển năm 1957.
4. Tham khảo
[1] Kruskal, Joseph B. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proceedings of the American Mathematical society 7.1 (1956): 48-50.
[2] Prim, Robert Clay. Shortest Connection Networks and some Generalizations. Bell System Technical Journal 36.6 (1957): 1389-1401.
[3] Borůvka, Otakar (1926). Příspěvek k řešení otázky ekonomické stavby elektrovodních sítí (Contribution to the Solution of a Problem of Economical Construction of Electrical Networks). Elektronický Obzor (in Czech) 15: 153–154.
[4] Nešetřil, Jaroslav, Eva Milková, and Helena Nešetřilová. Otakar Borůvka on minimum spanning tree problem translation of both the 1926 papers, comments, history. Discrete Mathematics 233.1 (2001): 3-36.
[5] Karger, David R.; Klein, Philip N.; Tarjan, Robert E. A Randomized Linear-time Algorithm to Find Minimum Spanning Trees. Journal of the ACM 42 (2): 321–328, 1995.
[6] Chazelle, Bernard. A Minimum Spanning Tree Algorithm with Inverse-Ackermann Type Complexity. Journal of the ACM (JACM) 47.6 (2000): 1028-1047.
[7]Jarník, V. O jistém problému minimálním” [About a certain minimal problem], Práce Moravské Přírodovědecké Společnosti (in Czech) 6: 57–63, 1930.
[8] Uri Zwick. Notes on Minimum Spanning Tree. Tel Aviv University, 2013.