Giải Thuật Tham Lam
Bài 7: Tham lam
Tham lam là một trong những phương pháp phổ biến nhất để thiết kế giải thuật. Tham lam thường là thuật toán dạng lặp, trong đó tại mỗi bước, ta xây dựng lời giải dần dần, cho đến khi thuật toán lặp kết thúc ta sẽ thu được lời giải cuối cùng của bài toán. Ý tưởng của tham lam, như cái tên đã gợi ý cho ta, là:
Rất nhiều thuật toán nổi tiếng được thiết kế dựa trên tư tưởng của tham lam, ví dụ như thuật toán tìm đường đi ngắn nhất của Dijkstra, thuật toán cây khung nhỏ nhất của Kruskal, v.v. Trong bài này chúng ta sẽ tìm hiểu nguyên lý thiết kế tham lam thông qua một vài ví dụ.
1. Lưu file trên đĩa từ
Bài toán như sau:
$C(\pi(i)) = \sum_{i=1}^{k} L[\pi(k)] $
Tìm cách lưu trữ file sao cho việc truy xuất được hiệu quả nhất, biết rằng mỗi file được truy cập đúng 1 lần.Ví dụ 1: Giả sử các file đánh số $1,2,3$ có dung lượng lần lượt là $5,4,6$. Nếu ta sắp xếp file theo thứ tự ${2,3,1}$ thì chi phí truy nhập là $4+10+15 = 29$. Nếu ta sắp theo thứ tự $2,1,3$ thì chi phí truy nhập là $4+9+15 =28$.
Ý tưởng của giải thuật tham lam như sau: giả sử ta đang sắp xếp file vào vị trí thứ $i$, để giảm chi phí truy nhập file thứ $i$, ta nên lưu trữ các vị trí $1,2,\ldots i-1$ bằng các file với tổng dung lượng nhỏ nhất. Cách lưu nào sẽ thoả mãn tính chất này với mọi $i$? Đó chính là lưu các file theo thứ tự từ nhỏ đến lớn theo dung lượng. Trong ví dụ 1, cách lưu $2,1,3$ có chi phí nhỏ hơn là vì nó là cách lưu theo thứ tự từ nhỏ đến lơn. Ta có giả mã như sau:
$S \leftarrow \{1,2,\ldots,n\}$
repeat
choose $s \in S$ with minimum $L[s]$
write $s$ to the tape
$S \leftarrow S \setminus \{s\}$
until $S = \emptyset$
Tính đúng đắn của thuật toán
Ta sẽ chứng minh cách lưu file theo thứ tự từ nhỏ đến lớn có chi phí nhỏ nhất. Giả sử tồn tại một cách lưu trữ tối ưu $\pi$ và chỉ số $i$ sao cho $L[\pi(i)] > L[\pi(i+1)]$. Gọi $cost_{\pi}$ là chi phí truy nhập của $\pi$. Theo định nghĩa, ta có: $cost_{\pi} = \sum_{i=1}^n C(\pi(i))$.
Gọi $\pi’$ là hoán vị thu được từ $\pi$ bằng cách đổi chỗ $\pi(i)]$ và $\pi(i+1)$. Ta có:
$\begin{array} {lcl} cost_{\pi} - cost_{\pi'} & = & C(\pi(i)) + C(\pi(i+1)) - C(\pi'(i)) - C(\pi'(i+1)) \\& = & L[\pi(i)] - L[\pi(i+1)] < 0 \end{array}$
Do đó, $cost_{\pi} > cost_{\pi’}$, trái với giả thiết $\pi(i)$ là cách lưu trữ tối ưu.
Phân tích thời gian
Bằng cách thực hiện sắp xếp theo chiều tăng của kích thước file, chúng ta có thể thực thi thuật toán trên trong thời gian $O(n\log n)$.
Bây giờ chúng ta hãy thay đổi bài toán một chút như sau:
$C(\pi(i)) =F[\pi(i)] \sum_{i=1}^{k} L[\pi(k)] $
Tìm cách lưu trữ file sao cho việc truy xuất được hiệu quả nhất.
Với bài toán này, tổng chi phí để truy xuất file là:
$Cost_{\pi} = \sum_{i=1}^n F[\pi(i)] \sum_{k=1}^iL[\pi(k)]$
Ví dụ 2: Giả sử các file đánh số $1,2,3$ có dung lượng lần lượt là $5,4,6$ với tần suất truy nhập là $2,1,1$. Nếu ta sắp xếp file theo thứ tự ${2,3,1}$ thì chi phí truy nhập là $4+10+2\times15 = 44$. Nếu ta sắp theo thứ tự $2,1,3$ thì chi phí truy nhập là $4+2\times 9+15 =37$.
Với bài toán tổng quát, trong ví dụ 2, ta vẫn thấy sắp xếp theo chiều tăng dần dung lượng có chi phí truy nhập rẻ hơn. Liệu đây có phải là cách tối ưu? Hay câu hỏi quan trọng hơn và tổng quát hơn:
Câu hỏi 1: khi tần số khác nhau, liệu sắp xếp file theo thứ tự tăng dần có phải là cách sắp xếp tối ưu?
Trả lời: Không. Xét hai file đánh số $1,2$ có dung lượng lần lượt là $1,2$ và tần số truy nhập là $1,10$. Nếu sắp xếp theo thứ tự $1,2$, thì chi phí truy nhập là $1 + 10\times (1+2) = 31$, trong khi sấp xếp theo thứ tự $2,1$ có chi phí truy nhập là $10\times 2 + 1 = 21$.
Câu trả lời trên gợi ý cho ta ý tưởng sau: lưu file có tần số truy nhập lớn hơn trước. Tuy nhiên, ý tưởng này vẫn chưa chuẩn, vì nếu các file có tần số bằng nhau, thì ta sẽ muốn lưu file có kích thước nhỏ trước. Từ đây ta chỉnh lại ý tưởng như sau:
Lưu file theo tỉ lệ $L[i]/F[i]$ tăng dần.
Trong câu trả lời cho câu hỏi 1, ta lưu theo thứ tự $2,1$ có chi phí thấp hơn vì tỉ lệ dung lượng / tần số của file 2 (là $2/10$) nhỏ hơn của file 1 (là $1/1$). Giả mã của thuật toán như sau:
$S \leftarrow \{1,2,\ldots,n\}$
repeat
choose $s \in S$ with minimum $\frac{L[s]}{F[s]}$
write $s$ to the tape
$S \leftarrow S \setminus \{s\}$
until $S = \emptyset$
Tính đúng đắn của thuật toán
Ta sử dụng ý tưởng tương tự trong trường hợp tần số bằng $1$. Giả sử tồn tại một cách lưu trữ tối ưu $\pi$ và chỉ số $i$ sao cho $\frac{L[\pi(i)]}{F[\pi(i)]} > \frac{L[\pi(i+1)]}{F[\pi(i+1)]}$. Gọi $\pi’$ là hoán vị thu được từ $\pi$ bằng cách đổi chỗ $L[\pi(i)]$ và $L[\pi(i+1)]$. Ta có:
$\begin{array} {lcl} Cost_{\pi} - Cost_{\pi'} & = & F[\pi(i)]C(\pi(i)) + F[\pi(i+1)]C(\pi(i+1)) \\ & & - F[\pi'(i)]C(\pi'(i)) - F[\pi'(i+1)]C(\pi'(i+1))\\ & = & F[\pi(i+1)]L[\pi(i)] - F[\pi(i)]L[\pi(i+1)] > 0 \end{array}$
vì $\frac{L[\pi(i)]}{F[\pi(i)]} > \frac{L[\pi(i+1)]}{F[\pi(i+1)]}$. Do đó, $Cost_{\pi} > Cost_{\pi’}$, trái với giả thiết $\pi(i)$ là cách lưu trữ tối ưu.
Phân tích thời gian
Bằng cách thực hiện sắp xếp theo chiều tăng của tỉ lệ kích thước / tần số, chúng ta có thể thực thi thuật toán trên trong thời gian $O(n\log n)$.
2. Bài toán chọn môn học
Ví dụ 2: ở hình dưới đây (lấy từ [1]), mỗi môn học được biểu diễn bởi một thanh ngang có chiều dài $F[i]-S[i]$. Tập các thanh màu xanh chính là một tập có số lượng lớn nhất các môn học không gối lên nhau:
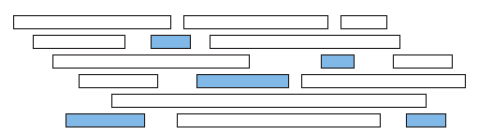
Ở đây ta có thể nghĩ đến 3 cách tham lam:
- Chọn lớp học bắt đầu sớm nhất trước. Tuy nhiên bạn có thể nghĩ ngay đến vấn đề của các chọn này là nếu có một lớp học bắt đầu sớm nhất nhưng lại kéo dài rất lâu thì bạn chỉ có thể chọn được 1 lớp học. Trong phần bài tập bạn sẽ phải tìm một phản ví dụ cho ý tưởng này.
- Chọn lớp học ngắn nhất trước. Vấn đề của các chọn này là nếu có một lớp học ngắn nhưng gối lên các lớp học bắt đầu trước và sau lớp học này, bạn sẽ không thể có phương án tối ưu. Trong phần bài tập bạn sẽ phải tìm một phản ví dụ cho ý tưởng này.
- Chọn lớp học có thời gian hoành thành sớm nhất trước. Có vẻ đây là một cách chọn tham lam tốt vì nếu chọn lớp hoàn thành sớm nhất trước, bạn sẽ có nhiều thời gian còn lại để chọn các lớp học khác. Thực tế đây là một cách chọn tham lam cho bạn phương án tối ưu.
Giả mã của thuật toán như sau:
1. sort $F$ in increasing order
2. permute indices of $S$ to match $F$
3. $J \leftarrow \{1\}$
4. tmp $\leftarrow $1
5. for $i \leftarrow 2 $ to $n$
6. if $F[tmp] \leq S[i]$ $\ll$ class $i$ does not confict with tmp $\gg$
7. tmp $\leftarrow$ i
8. $J \leftarrow J \cup \{i\}$
9. return $J$
Tính đúng đắn của thuật toán
Giả sử $X = {x_1,x_2,\ldots, x_k}$ là tập các lớp học đầu ra của thuật toán tham lam và $Y = {y_1,y_2,\ldots, y_m }$ là một phương án tối ưu ($k \leq m$), sắp xếp theo chiều tăng dần của thời gian hoành thành. Gọi $Y_k = {y_1,y_2,\ldots,y_k} \subseteq Y$ là tập $k$ phần tử đầu tiên của $Y$. Trong số các phương tối ưu, chọn phương án $Y$ sao cho $|X \cap Y_k|$ là lớn nhất.
Nếu $X = Y_k$, ta có $m = k$ vì nếu không, giải thuật tham lam sẽ thêm ít nhất một lớp học nữa vào $X$. Do đó, $X$ là một phương án tối ưu. Giả sử $X \not= Y_k$. Suy ra tồn tại $1 \leq i \leq k$ sao cho $y_i \not= x_i$. Ta chọn $i$ nhỏ nhất thỏa mãn $y_i \not= x_i$. Như vậy $y_j = x_j, 1 \leq j \leq i-1$. Do $x_i$ là lớp học có thời gian hoành thành sớm nhất sau khi $x_{i-1}$ đã hoàn thành, thời gian hoành thành của $x_i$ sớm hơn $y_i$. Suy ra $x_{i}$ kết thúc trước khi $y_{i+1}$ bắt đầu. Không khó để chứng minh được $y_i \not\in X$ (xem phần bài tập).
Xét $Y’ = Y \setminus {y_i} \cup {x_i}$. Cụ thể
$Y' = \{x_1,x_2,\ldots, x_{i-1}, x_i, y_{i+1}, \ldots, y_m\}$
Dễ thấy, $|Y’| = Y = m$ và các lớp trong $Y’$ không gối lên nhau. Do đó $Y’$ là một phương án tối ưu. Tuy nhiên $|X \cap Y’_k| > |X \cap Y_k|$, trái với cách chọn $Y$ là phương án có $|X \cap Y_k|$ lớn nhất. Do đó, $X$ là phương án tối ưu.
Phân tích thời gian
Dòng 1 của thuật toán có thời gian $O(n \log n)$. Dòng thứ 2 có thể thực hiện được trong thời gian $O(n)$. Bằng cách thực hiện sắp xếp theo chiều tăng của tỉ lệ kích thước / tần số, chúng ta có thể thực thi thuật toán trên trong thời gian $O(n\log n)$. Ta có thể dùng một danh sách liên kết để lưu trữ $J$, do đó dòng 5 đến 8 có thể thực hiện trong thời gian $O(n)$. Tóm lại, tổng thời gian của thuật toán là $O(n\log n)$.
Phương pháp chứng minh bằng phản chứng cho bài toán chọn lớp học cũng là một phương pháp chứng minh phổ biến để chứng minh thuật toán tham lam là tối ưu. Ta có thể rút ra các bước như sau:
- Giả sử lời giải tham lam $X$ là không tối ưu. Chọn lời giải tối ưu $Y$ khác $X$ với $|Y\cap X|$ lớn nhất.
- Xét hai phần tử khác nhau đầu tiên giữa hai lời giải này.
- Chứng minh bằng bằng cách trao đổi hai phần tử khác nhau đầu tiên, ta thu được một lời giải tối ưu khác $Y'$ có $|X\cap Y| > |X \cap Y|$, qua đó, ta thu được phản chứng.
Bạn có thể thử phương pháp trên cho bài toán lưu trữ file trên đĩa từ.
3. Tham khảo
[1] Jeff Erickson. Greedy Algorithm Lecture Notes, UIUC.
[2] George Kocur, MIT OWC lecture notes, MIT.
[3] Cormen, Thomas H.; Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford.Introduction to Algorithms (2nd ed.) . MIT Press and McGraw-Hill (2001). ISBN 0-262-03293-7.
Ghi chú: Cám ơn bạn Huy Nguyen đã chỉ ra nhiều lỗi và góp ý trên bài viết gốc.
4. Bài tập
Bài 1: Tìm cách sắp xếp tối ưu cho tập các file trong ví dụ $2$.
Bài 2: Tìm phản ví dụ cho ý tưởng 1 trong phần 2, bài toán chọn môn học.
Bài 3: Tìm phản ví dụ cho ý tưởng 2 trong phần 2, bài toán chọn môn học.
Bài 4: Chứng minh rằng $y_i \not\in X$ trong chứng minh tính đúng đắn của thuật toán tham lam trong bài toán chọn môn học.
Bài 5: Thực thi cả hai thuật toán trong phần 1 và 2 bằng ngôn ngữ C.
Bài 6: Bạn được ông chủ giao cho $n$ tác vụ và một chiếc máy tính để thực hiện $n$ tác vụ đó. Tác vụ thứ $i$ có thời hạn $D[i]$ và nếu bạn hoành thành tác vụ đó trước thời hạn $D[i]$, bạn sẽ được thưởng $P[i]$ đồng, còn nếu hoành thành sau $D[i]$, bạn sẽ chẳng nhận được đồng tiền thưởng nào cả. Biết rằng mỗi tác vụ mất thời gian đúng 1 đơn vị để hoành thành. Tìm một cách thực thi các tác vụ sao cho bạn nhận được nhiều tiền thưởng nhất. Giả sử thời hạn của các tác vụ là trong khoảng $[1,n]$.
Ví dụ bạn có 5 tác vụ với thông tin như sau:
| Job | Profit | Deadline |
| 1 | 100 | 2 |
| 2 | 19 | 1 |
| 3 | 27 | 2 |
| 4 | 25 | 1 |
| 5 | 15 | 3 |
Phương án tối ưu là (theo trình tự thực thi) ${1,3,5}$ với tổng tiền thưởng thu được là 142.
- Thiết kế thuật toán tham lam giải bài toán trên.
- Phân tích tính đúng đắn và thời gian chạy của thuật toán đã thiết kế.