Hệ Thức Truy Hồi
Bài 2: Giải hệ thức truy hồi
Trong bài này, chúng ta tìm hiểu một số cách giải công thức truy hồi mà chúng ta hay gặp trong phân tích thuật toán. Rất nhiều hệ thức truy hồi xuất hiện trong phân tích thuật toán có thể quy được về một trong hai bài toán tổng quát sau:
Bài toán 1: Giải hệ thức truy hồi: \begin{aligned} T(n) = aT(\frac{n}{b}) + f(n) \qquad (1) \end{aligned} trong đó $a,b$ là các hằng số dương.
và
Bài toán 2: Giải hệ thức truy hồi: \begin{aligned} T(n) = \sum_{i=1}^k a_iT(\frac{n}{b_i}) + f(n)\qquad (2) \end{aligned} trong đó $a_i,b_i, i = 1,\ldots, k$ là các hằng số dương.
Trong bài này, chúng ta sẽ tìm hiểu 3 phương pháp giải. Mỗi phương pháp có ưu và nhược điểm riêng của nó. Ta bắt đầu với phương pháp đơn giản nhất.
1. Phương pháp đoán
Đây có lẽ là phương pháp mà chúng ta thường hay nghĩ tới khi bắt gặp một hệ thức truy hồi.
Nguyên lý: Dự đoán kết qủa và chứng minh bằng phương pháp quy nạp.
Theo nguyên lý, ta chỉ đơn giản giải hệ thức truy hồi bằng cách đoán nghiệm, thử chứng minh và đoán lại. Để minh hoạ, xét một vài ví dụ sau.
Ví dụ 1 Tìm công thức tổng quát của $T(n)$ biết rằng: \begin{aligned} T(n) = 2T(n-1) + 1 \qquad \qquad T(1) = 1 \end{aligned}
Thử một vài giá trị đầu tiên, ta thấy: \begin{aligned} T(2) = 3, T(3) = 7, T(4) = 15, \ldots \end{aligned} Không khó để nhận ra 3 giá trị đầu thoả mãn quy luật: $T(2) = 2^2-1$, $T(3) = 2^3-1$, $T(4) = 2^4-1$. Do đó, ta có thể dự đoán $ T(n) = 2^n -1$.
Chứng minh: Theo giả thiết quy nạp, ta có $T(n-1) = 2^{n-1}-1$. Do đó: \begin{aligned} T(n) = 2T(n-1) + 1 = 2(2^{n-1}-1) + 1 = 2^n -1\end{aligned} Đây là dpcm.
Bây giờ chúng ta thử áp dụng cho bài toán khó hơn
Ví dụ 2: Tìm công thức tổng quát của $T(n)$ biết rằng: \begin{aligned} T(n) = \sqrt{n}T(\sqrt{n}) + n \qquad \qquad T(1) = \Theta(1) \end{aligned}
Trong hệ thức trên, $T(1) = \Theta(1)$ mang ý nghĩa $T(1)$ là một hằng số $c$ nào đó (ví dụ 2, 3 hay 5). Với mỗi hằng số, khi giải hệ thức, ta tìm được một $T(n)$ khác nhau. Như vậy ta nên chọn hằng số nào để giải hệ thức trong ví dụ 2? Thực ra ta chỉ quan tâm đến giá trị tiệm cận của $T(n)$ theo biến $n$ chứ không phải một biểu thức chính xác của $n$. Xem lại bài tiệm cận tại đây.
Dự đoán 1 : $ T(n) = O(n \log n)$.
Ghi chú 1: bạn có thể hỏi tại sao lại đoán $O(n\log n)$; thực ra ở đây ta cứ chọn bừa một biểu thức mà ta cảm thấy hợp lý; thay vào đó, bạn có thể chọn dự đoán $O(n^2)$.
Giờ ta thử chứng minh $T(n) \leq a n\log n$. Điểm mấu chốt ở đây là khái niệm $O(.)$ cho phép ta tùy ý chọn chọn hằng số $a$ và giá trị bé nhất của $n$ để dự đoán của chúng ta là đúng. \begin{aligned} T(n) = \sqrt{n}T(\sqrt{n}) + n \leq \sqrt{n}\cdot a\sqrt{n}\log \sqrt{n} +n \leq a n\log n \end{aligned} Ở bất đẳng thức cuối, ta giả sử $ n \geq 2^{2/a} $. Như vậy, dự đoán của chúng ta là đúng.
Ghi chú 2: Có vẻ như ta đang “tuỳ tiện” giả sử $n \geq 2^{2/a}$. Thực ra đây không phải là một giả sử tuỳ tiện. Bạn có thể giả sử $n$ “lớn tuỳ ý”. Để hiểu tại sao ta lại được phép giả sử như vậy, bạn cần xem lại định nghĩa của big-O.
Bây giờ chúng ta thử chứng minh cận dưới $T(n) \geq bn\log n$ bằng quy nạp với $b$ là một hằng số nào đó. \begin{aligned} T(n) = \sqrt{n}T(\sqrt{n}) + n \geq \sqrt{n}\cdot b\sqrt{n}\log \sqrt{n} +n = \frac{b}{2} n\log n + n \end{aligned}
Giá trị này lớn hơn $b n \log n$ khi và chỉ khi $n \geq b/2 n\log n$. Điều này là không thể xảy ra vì với mọi giá trị của hằng số $b$, luôn tồn tại $n$ đủ lớn để $ \frac{b}{2} n\log n < n$. Như vậy, cận trên $O(n\log n)$ vẫn chưa chặt.
Dự đoán 2: $T(n) = O(n)$. Ta lặp lại ý tưởng ở trên, thử chứng minh $ T(n) \leq a n$. \begin{aligned} T(n) = \sqrt{n}T(\sqrt{n}) + n \leq \sqrt{n}\cdot a\sqrt{n} +n = (a+1) n \nleq a n \end{aligned} Như vậy dự đoán chúng ta là sai.
Dự đoán 3: $ T(n) = O(n\sqrt{n})$. Chứng minh tương tự như dự đoán 1 ta thấy dự đoán này đúng. Tuy nhiên, nếu cố gắng chứng minh cận dưới $ T(n) = \Omega (n\sqrt{n})$ chúng ta sẽ gặp vấn đề.
Ghi chú 3: Thực ra ta đã chứng minh $T(n) = O(n \log n)$, và vì $n\log n = O(n\sqrt{n})$ nên hiển nhiên $T(n) = O(n\sqrt{n})$. Xem lại Tính chất 1 của bài tiệm cận.
Dự đoán 4: $T(n) = O(n\log\log n)$. Chứng minh cận trên $ T(n) \leq a n\log\log n $:
\begin{array} {lcl} T(n) & = & \sqrt{n}T(\sqrt{n}) + n \\ & \leq & \sqrt{n}\cdot a\sqrt{n} \log\log \sqrt{n} +n \\ & = & a n\log\log n -a n + n \\ & \leq & a n \log\log n\end{array}
khi $a \geq 2$. Giờ ta chỉ cần chứng minh cận dưới $T(n) \geq b n\log\log n$:
\begin{array} {lcl} T(n) & = & \sqrt{n}T(\sqrt{n}) + n \\ & \geq & \sqrt{n}\cdot b\sqrt{n} \log\log \sqrt{n} +n \\ & = & b n\log\log n -b n + n \\ & \geq & b n \log\log n \qquad \mbox{nếu } b \leq 1\end{array}
Do đó, ta có thể kết luận $T(n) = \Theta(n\log\log n)$.
Định lý thợ
Định lý thợ (master theorem) là một công cụ giúp ta giải các hệ thức truy hồi có dạng trong bài toán 1. Định lý dài và khó nhớ và theo mình bạn đọc cũng không cần nhớ làm gì. Chỉ cần nhớ dạng bài toán mà định lý này có thể áp dụng để giải. Nếu có thể thì chỉ cần nhớ phương pháp chứng minh định lý.
- Nếu $ af(n/b) = \kappa f(n)$ với $ \kappa < 1$, ta có $T(n) = \Theta(f(n))$.
- Nếu $ af(n/b) = K f(n)$ với $ K > 1$, ta có $ T(n) = \Theta(n^{\log_b a})$.
- Nếu $ af(n/b) = f(n)$, ta có $ T(n) = \Theta(f(n)\log_b n)$.
Chứng minh: Chúng ta sử dụng phương pháp cây đệ quy. Cây đệ quy có nút gốc có giá trị $ f(n)$ và $ a$ nút con. Mỗi nút con của nút gốc sẽ là gốc của một cây cho hàm đệ quy $ T(n/b)$. Như vậy, ở độ sâu thứ $ i$, giá trị của hàm của các nút là $ f(n/b^i)$. Xem minh hoạ trong hình 1.
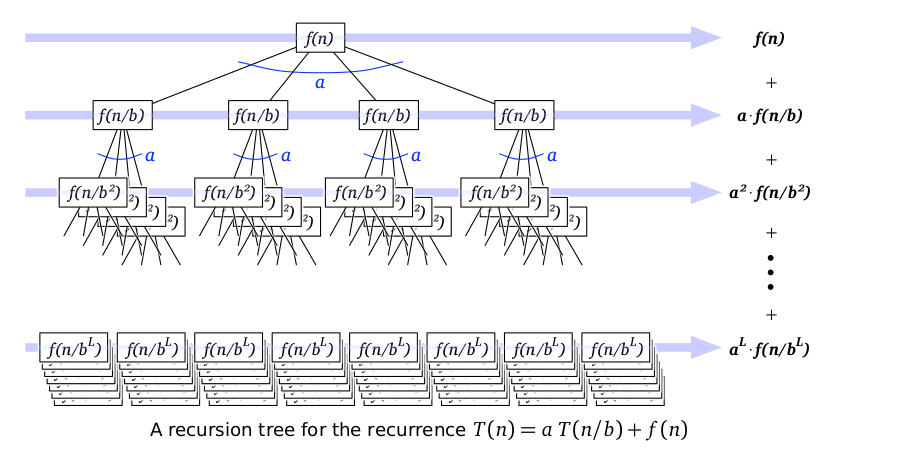
Hình 1: Minh hoạ cây đệ quy giải hệ thức truy hồi trong định lý thợ. Hình được cắt từ tài liệu tham khảo [1].
Sử dụng cây đệ quy ta suy ra: \begin{aligned}T(n) = \sum_{i=1}^L a^i f(\frac{n}{b^i})\qquad (1)\end{aligned} Ở đây $ L$ là độ sâu của cây đệ quy. Dễ thấy, $ L = \log_b n$ do mỗi lần đi xuống sâu thêm một mức của cây đệ quy, giá trị của $n$ giảm đi $b$ lần. Xét trường hợp:
- TH1: $ af(n/b)= f(n)$, ta có $ a^if(n/b^i) = f(n)$. Điều này có nghĩa là tổng giá trị tại mỗi mức của cây là $f(n)$. Do cây có $L$ mức, ta suy ra: \begin{aligned}T(n) = \Theta(f(n) L) = \Theta(f(n)\log_b n).\end{aligned}
- TH2: $af(n/b)= \kappa f(n)$. Sử dụng phương pháp quy nạp, ta có \begin{aligned}a^i f(n/b^i) = a(a^{i-1}f(\frac{n/b}{b^{i-1}})) = a(\kappa^{i-1}f(n/b)) = \kappa^i f(n).\end{aligned} Do đó, $ T(n) = f(n) \sum_{i=1}^{L} \kappa^i = \Theta(f(n))$ vì $\kappa < 1 $ ( xem thêm về geometric series).
- TH3: $af(n/b)= K f(n)$, sử dụng phương pháp quy nạp tương tự TH2, ta suy ra $ a^if(n/b^i) = K^i f(n)$. Như vậy, \begin{aligned}T(n) = f(n) \sum_{i=1}^{L} K^i = \Theta(f(n)K^{L+1}) = \Theta(n^{\log_b(K)}) = \Theta(n^{\log_b(a)}).\end{aligned} Phương trình cuối là do $K \leq a$ vì $af(n/b)\leq a f(n)$ do $f(.)$ là một hàm đơn điệu tăng theo $n$ khi $n$ đủ lớn.
Ta xét một vài ví dụ ứng dụng.
Ví dụ 3: Tìm tiệm cận của $T(n)$ biết rằng $T(n) = 2T(n/2) + n$.
Lời giải: Do $af(n/b) = 2(n/2) = n = f(n)$, theo định lý thợ, ta có $T(n) = O(f(n)\log n) = O(n\log n)$.
Trong ví dụ 3, ta cũng có thể dùng công thức trong phương trình (1) để tính. Cụ thể, $T(n) = \sum_{i=1}^L 2^i n/2^i = \sum_{i=1}^L n = \Theta(n\log n)$.
Ví dụ 4: Tìm tiệm cận của $T(n)$ biết rằng $T(n) = 3T(n/2) + n$.
Lời giải: Do $af(n/b) = 3(n/2) = 1.5 n = Kf(n)$ với $K = 1.5$, theo định lý thợ, ta có $T(n) = O(n^{\log_b a}) =O( n^{\log_2 3})$.
Nếu sử dụng công thức (1) trong ví dụ 4, ta có: \begin{aligned}T(n) = \sum_{i=1}^L 3^i n/2^i = n\sum_{i=1}^{\log_2 n} (3/2)^i = n (3/2)^{\log_2n} = n^{\log_2 3}. \end{aligned}
Ví dụ 5: Tìm tiệm cận của $T(n)$ biết rằng $T(n) = \sqrt{n}T(\sqrt{n}) + n$.
Lời giải: Do dạng của phương trình đệ quy này không giống với dạng trong định lý thợ, ta không thể áp dụng công thức tổng quát của định lý thợ. Tuy nhiên, ta có thể áp dụng trực tiếp phương pháp cây đệ quy. Nhìn vào cây nhị phân, ta thấy tổng giá trị mỗi mức là $n$. Do đó, $T(n) = \sum_{i=1}^L n$ với chiều cao cây $L$. Không khó để thấy rằng $L$ thỏa mãn phương trình $n^{2^{-L}} = \Theta(1)$. Giải ra ta được $L = \Theta(\log\log n)$. Như vậy $T(n) = \Theta (n \log\log n)$.
Ghi chú 4: Định lý thợ khá dài dòng và khó nhớ. Thực ra ta không nhất thiết phải nhớ chi tiết định lý này. Hai điều cần nhớ từ định lý này là: (a) có một công thức tổng quát để ta có thể tra cứu và đối chiếu khi cần dùng và (b) phương pháp cây đệ quy để giải hệ thức truy hồi. Về bản chất, phương pháp cây nhị phân mới là điều cần ghi nhớ ở đây.
Phương pháp “bom tấn”
Trong phần này chúng ta sẽ tìm hiểu một công cụ rất mạnh để giải công thức đệ quy có dạng trong bài toán 2. Phương pháp được đề xuất bởi Mohamad Akra và Louay Bazzi năm 1998. Với điều kiện $k,a_i,b_i$ là các hằng số, lời giải của bài toán 2 có dạng như sau:
Trong đó $\rho$ thỏa mãn phương trình:
Bạn đọc có thể tham khảo chứng minh của định lí này trong [2].
Ví dụ 6: Tìm tiệm cận của $T(n)$ biết rằng \begin{aligned}T(n) = T(3n/4) + T(n/4) + n.\end{aligned}
Lời giải: Áp dụng phương trình (2), ta tìm $\rho$ thỏa mãn phương trình (3): $(3/4)^\rho + (1/4)^\rho = 1$. Dễ thấy lời giải ở đây là $\rho = 1$. Do đó, ta có: \begin{aligned} T(n) = \Theta(n(1 + \int_{1}^n \frac{u}{u^2}du)) = O(n\log n)\end{aligned}
Ví dụ 7: Tìm tiệm cận của $T(n)$ biết rằng \begin{aligned}T(n) = T(n/5) + T(7n/10) + n.\end{aligned}
Lời giải: Ta tìm $\rho$ thỏa mãn: $(1/5)^\rho + (7/10)^\rho = 1$. Không khó để thấy $\rho$ sẽ là một số nằm trong khoảng $(0,1)$. (Ta có thể sử sử dụng wolframalpha để tìm $\rho$). Áp dụng công thức tổng quát ta có:
$ T(n) = \Theta(n^{\rho}(1 + \int_{1}^n \frac{u}{u^{\rho + 1}}du)) = \Theta(n^{\rho}(1 + \Theta(n^{1 -\rho}) ) = \Theta(n)$
Tham khảo
[1] J. Erickson, Note on Recurrence Relation, UIUC, Fall 2013.
[2] T. Leighton: Notes on Better Master Theorems for Divide-and-Conquer Recurrences , Manuscript. MIT, 1996.
Bài tập
Bài tập 1: Tìm giá trị tiệm cận của các hàm sau:
- $A(n) = A(n-1) + 1 \qquad A(0)=0$.
- $B(n) = B(n-1) + \frac{1}{n} \qquad B(0) = 0$.
- $C(n) = C(n-2) + \frac{3}{n} \qquad C(0) = C(1) = 0$.
- $D(n) = (D(n-1))^2 \qquad D(0) = 2$.
- $E(n) = E(n-1)E(n-2) \qquad E(0) = 2, E(1)=1$ (gợi ý: viết lời giải dưới dạng dãy số Fibonacci.).
Bài tập 2: Sử dụng định lý thợ, tìm tiệm cận của các hàm sau:
- $A(n) = A(n/2) + O(1)$.
- $B(n) = 4B(n/2) + O(n)$.
- $C(n) = 3C(n/2) + O(n)$.
- $D(n) = 7 D(n/2) + O(n^2)$.
Bài tập 3: Sử dụng cây đệ quy hoặc phương pháp bom tấn để tìm giá trị tiệm cận của các hàm sau:
- $A(n) = 2A(n/4) + \sqrt{n}$.
- $B(n) = 2B(n/4) + n$.
- $C(n) = 2C(n/4) + n^2$.
- $D(n) = \sqrt{2n}D(\sqrt{2n}) + \sqrt{n}$.
- $E(n) = 2E(n/3) + 2E(2n/3) + n$.
- $F(n) = 2 F(n/2) + O(n\log n)$.
Bài tập 1 được lấy từ Jeff Erickson Notes và bài tập 3 lấy từ Introduction to Algorithm, 2nd.