Khái Niệm Tiệm Cận
Bài 1: Khái niệm tiệm cận
Phân tích (thời gian) thuật toán về cơ bản là đếm số thao tác cơ bản mà thuật toán thực hiện. Tuy nhiên, việc đếm chính xác số thao tác cơ bản nhiều lúc không tầm thường hoặc phụ thuộc vào dữ liệu đầu vào (ví dụ lệnh if-then-else). Do đó, trong thực tế phân tích thuật toán, ta chỉ đếm tương đối số thao tác cơ bản mà thôi. Khái niệm big-O, kí hiệu $O(.)$, chính là một công cụ cho phép chúng ta biểu diễn tương đối độ phức tạp của thuật toán một cách đơn giản. Bài này chúng ta sẽ tìm hiểu định nghĩa hình thức của các khía niệm $O(.), o(.), \Omega(.), \Theta(.)$. Bạn đọc có thể tham khảo trước ý nghĩa các khái niệm này cũng nhưng các sử dụng trong phân tích thuật toán thực tế.
Trong các kí hiệu dưới đây, $T(n)$ biểu thị một hàm số của biến (số nguyên) $n$. Thông thường ta dùng $T(n)$ để kí hiệu thời gian tính toán của một thuật toán.
1. Kí hiệu big-O.
Định nghĩa 1: Ta viết $T(n) = O(f(n))$ nếu tồn tại hằng số $c , n_0 > 0$ sao cho $T(n) \leq cf(n)$ với mọi $n \geq n_0.$
Để hiểu định nghĩa 1, ta xét hai ví dụ:
Ví dụ 1: Cho $T(n) = 3n^2 + 2n +4$. Theo định nghĩa 1, ta suy ra $T(n) = O(n^2)$ vì $3n^2 + 2n +4 \leq 9n^2$ với mọi $n \geq 1$. Ở đây ta chọn $c= 9, n_0 = 1$.
Ví dụ 2: Cho $T(n) = 3n^2 + 2n +4$. Theo định nghĩa 1, ta có thể viết $T(n) = O(n^3)$ vì $3n^2 + 2n +4 \leq 9n^3$ với mọi $n \geq 1$. Ở đây ta chọn $c= 9, n_0 = 1$.
Trong cả hai ví dụ ta đều xét cùng một biểu thức $T(n) = 3n^2 + 2n +4$, và theo định nghĩa 1, viết $T(n) = O(n^2)$ và $T(n) = O(n^3)$ đều đúng. Câu hỏi đặt ra là ta nên chọn cách viết nào? Thông thường ta sẽ chọn cách viết thể hiện “đúng nhất” bản chất tăng/giảm của hàm $T(n)$. Do đó, trong trường hợp này ta nên viết $T(n) = O(n^2)$. Khái niệm big-O thường phù hợp để phân tích cận dưới của thời gian tính toán của một thuật toán.
Từ định nghĩa, ta dễ dàng suy ra tính chất sau:
Tính chất 1: Nếu $T(n) = O(f(n))$ và $f(n) = O(g(n))$ thì $T(n) = O(g(n))$.
Chứng minh: Theo định nghĩa 1, tồn tại hai hằng số (dương) $c_1$ và $n_1$ sao cho $T(n) \leq c_1f(n)$ với mọi $n\geq n_1$. Cũng theo định nghĩa 1, tồn tại hai hằng số $c_2$ và $n_2$ sao cho $f(n) \leq c_2g(n)$ với mọi $n\geq n_2$. Chọn $c_3 = c_1\cdot c_2$ và $n_3 = \max(n_1,n_2)$, ta suy ra $T(n) \leq c_3 g(n)$ với mọi $n\geq n_3$ (dpcm).
2. Kí hiệu $\Omega$
Định nghĩa 2: Ta viết $T(n) = \Omega(f(n))$ nếu tồn tại hai hằng số $c , n_0> 0$ sao cho $T(n) \geq cf(n)$ với mọi $n \geq n_0$.
Xét hai ví dụ áp dụng sau:
Ví dụ 3: Cho $T(n) = 3n^2 + 2n +4$. Theo định nghĩa 2, ta suy ra $T(n) = \Omega(n^2)$ vì $3n^2 + 2n +4 \geq 3n^2$ với mọi $n \geq 1$. Ở đây ta chọn $c= 3, n_0 = 1$.
Ví dụ 4: Cho $T(n) = 3n^2 + 2n +4$. Theo định nghĩa 2, ta suy ra $T(n) = \Omega(n)$ vì $3n^2 + 2n +4 \geq n$ với mọi $n \geq 1$. Ở đây ta chọn $c= 1, n_0 = 1$.
Ví dụ 3 và 4 cung cấp hai cách viết khác nhau cho cùng một hàm $T(n)$, và tương tự như phần 1, ta thường chọn cách viết “gần nhất”. Có nghĩa là ở đây ta nên viết $T(n) = \Omega(n^2)$. Khái niệm $\Omega$ thường phù hợp để phân tích cận dưới của thời gian tính toán của một thuật toán.
Tính chất 2: Nếu $T(n) = \Omega(f(n))$ và $f(n) = \Omega(g(n))$ thì $T(n) = \Omega(g(n))$.
Chứng minh tương tự như tính chất 1; ta coi đây là bài tập cho bạn đọc.
3. Kí hiệu $\Theta$
Định nghĩa 3: Ta viết $T(n) = \Theta(f(n))$ nếu $T(n) = O(f(n))$ và $T(n) = \Omega(f(n))$.
Ví dụ 5: Cho $T(n) = 3n^2 + 2n +4$. Theo định nghĩa 3, $T(n) = \Theta(n^2)$ vì $T(n) = O(n^2)$ (theo định nghĩa 1) và $T(n) = \Omega(n^2)$ (theo định nghĩa 2).
Như vậy, nếu $T(n) = \Theta(f(n))$, thì về mặt trực quan, thuật toán đó có thời gian chạy “đúng” là $f(n)$. Khái niệm $\Theta$ phù hợp để phân tích cả cận trên và cận dưới của thuật toán. Khi phân tích thuật toán, lý tưởng nhất là ta có thể biểu diễn thời gian bằng kí hiệu $\Theta(f(n))$ của một hàm $f(n)$ đơn giản nào đó, ví dụ như $n^2$ hay $n \log n$. Tuy nhiên, với hầu hết các bài toán phân tích và thiết kế, hiếm khi ta có thể chứng minh được thời gian là $\Theta(f(n))$.
Một câu hỏi cho bạn đọc tự suy nghẫm: nếu viết hàm $T(n)$ trong ví dụ 5 là $T(n) = \Theta(n^3)$ thì có đúng hay không?
4. Kí hiệu $o$
Định nghĩa 4: Ta viết $T(n) = o(f(n))$ nếu với mọi hằng số $c > 0$, tồn tại hằng số $ n_0 > 0$ sao cho: $T(n) \leq cf(n)$ với mọi $n \geq n_0.$
Chú ý, hằng số $n_0$ có thể phụ thuộc vào $c$. Xét ví dụ áp dụng sau:
Ví dụ 6: Cho $T(n) = 3n^2 + 2n +4$. Theo định nghĩa 4, ta có thể viết $T(n) = o(n^3)$ vì với mọi hằng số $c > 0$ bất kì, ta có thể chứng minh được $T(n) \leq c\cdot n^3$ với mọi $n\geq \max(\frac{9}{c}, 1)$; ở đây ta chọn $n_0 = \max(\frac{9}{c}, 1)$. Thật vậy:
Ý nghĩa của $o(.)$ đó là nếu $T(n) = o(f(n))$ thì $T(n)$ tăng chậm hơn $f(n)$ “rất nhiều” khi $n$ đủ lớn.
Hình sau minh hoạ các khái niệm trong bài này một cách trực quan hơn.
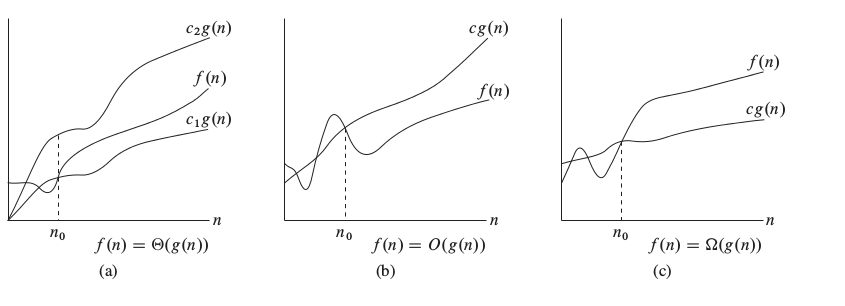
Hình (a) minh hoạ trường hợp $f(n) = \Theta(g(n))$. Khi $n\geq n_0$ thì đường cong $f(n)$ sẽ nằm giữa hai đường cong $c_1 g(n)$ và $c_2 g(n)$ với $c_2 \geq c_1$ là hai hằng số (nào đó). Hình (b) minh hoạ trường hợp $f(n) = O(g(n))$. Khi $n\geq n_0$ thì đường cong $f(n)$ sẽ nằm dưới đường cong $c g(n)$ với $c$ là một hằng số (nào đó). Hình (c) minh hoạ trường hợp $f(n) = \Omega(g(n))$. Khi $n\geq n_0$ thì đường cong $f(n)$ sẽ nằm trên đường cong $c g(n)$ với $c$ là một hằng số (nào đó). (Hình được lấy từ tài liệu tham khảo [1].)
5. Tham khảo
[1] Cormen, Thomas H.; Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford (2001) [1990]. Introduction to Algorithms (2nd ed.) . MIT Press and McGraw-Hill. ISBN 0-262-03293-7.
[2] Avrim Blum: Lecture notes on Algorithms, http://www.cs.cmu.edu/afs/cs/academic/class/15451-f11/www/lectures/lects1-10.pdf . Carnegie Mellon University, 2011.
6. Bài tập
Bài tập 1: Cho $T(n) = 2n + 1$.
- (a) Chứng minh rằng $T(n) = O(n^2)$.
- (b) Nếu viết $T(n) = O(n)$ thì có sai không?
- (c) Nếu viết $T(n) = O(\sqrt{n})$ thì có sai không?
Bài tập 2: Cho $T(n) = n! + 3n$.
- (a) Chứng minh rằng $T(n) = \Omega(2^n)$.
- (b) Nếu viết $T(n) = O(10^n)$ thì có sai không?
- (c) Nếu viết $T(n) = O(n^n)$ thì có sai không?
Bài tập 3: Cho $T(n) = \log(n!)$. Chứng minh rằng $T(n) = \Theta(n \log n)$ với cơ số của logarith là $2$.
Bài tập 4: Hàm $f(n)$ được gọi là tăng nhanh hơn hàm $g(n)$ nếu $g(n) = O(f(n))$. Sắp xếp các hàm sau theo thứ tự tăng dần của độ tăng.
- (a) $(\frac{3}{2})^n \quad n^3 \quad \log^2 n \quad \log (n!) \quad 2^{2^n} \quad n^{\frac{1}{\log n}}$.
- (b) $(2)^{\log n} \quad (\log n)^{\log n} \quad e^n \quad 4^{\log n} \quad (n+1)! \quad \sqrt{\log n}$.
Bài tập 5: Chứng minh tính chất 2 phát biểu ở trên.
Bài tập 6: Những kết luận sau đúng hay sai? Chứng minh.
- (a) $f(n) = O(g(n))$ suy ra $g(n) = O(f(n))$.
- (b) $f(n) + g(n) = \Theta(\min(f(n),g(n)))$.
- (c) $f(n) = O(g(n))$ suy ra $2^{f(n)} = O(2^{g(n)})$.
- (d) $f(n) = \Theta(f(n/2))$.
Bài tập 7: Nếu $T(n) = \Theta(f(n))$, chứng minh rằng tồn tại ba hằng số $c_1,c_2 , n_0 > 0$ sao cho: $c_1f(n) \leq T(n) \leq c_2f(n)$ với mọi $n \geq n_0.$
Bài tập 8: $T(n) = \Theta(f(n))$ khi và chỉ khi $\lim_{n \rightarrow \infty} \frac{T(n)}{f(n)} = c$ với $c$ là một hằng số lớn hơn 0.
Bài tập 9: Chứng minh rằng $T(n) = o(f(n))$ khi và chỉ khi $\lim_{n \rightarrow \infty} \frac{T(n)}{f(n)} = 0$.