Nhập Môn Đồ Thị
Bài 10: Nhập môn đồ thị
Trong bài này và loạt bài tiếp theo chúng ta sẽ làm quen với đồ thị, cách biểu diễn và duyệt đồ thị. Trong các bài tiếp theo, ta sẽ tìm hiểu một số bài toán khác thú vị hơn liên quan tới đồ thị.
1. Các khái niệm
Một đồ thị, kí hiệu là $G(V,E)$, gồm hai thành phần:
- Tập hợp $V$, bao gồm các đối tượng, được gọi là tập hợp các đỉnh của đồ thị
- Tập hợp $E \subseteq V\times V$, bao gồm một cặp các đỉnh, được gọi là tập hợp các cạnh của đồ thị
Ta sẽ kí hiệu $n,m$ lần lượt là số đỉnh và số cạnh của đồ thị, i.e, $|V| = n, |E|= m$.
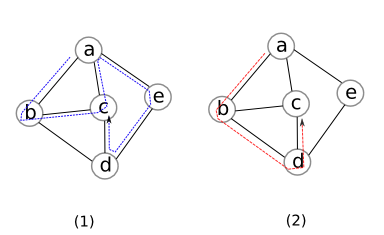
Các đỉnh ta sẽ kí hiệu bằng các chữ in thường như $u,v,x,y,z$. Cạnh giữa hai đỉnh $u,v$ có thể là vô hướng hoặc có hướng. Trong trường hợp đầu ta sẽ kí hiệu cạnh là $uv$, còn trong trường hợp sau ta sẽ kí hiệu là $u \rightarrow v$ để chỉ rõ hướng của cạnh là từ $u$ đến $v$. Thông thường khi ta nói cạnh thì ta ám chỉ cạnh vô hướng còn với một cạnh có hướng ta sẽ gọi nó là một cung (arc). Hình $(1,2)$ của hình dưới đây biểu diễn một đồ thị vô hướng (các cạnh là vô hướng) và hình $(3)$ phải của hình dưới đây biểu diễn một đồ thị có hướng.
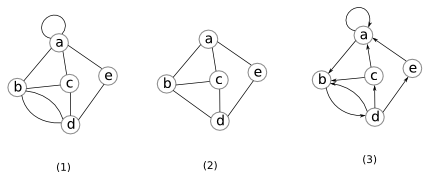
Trong hình $(1)$, cạnh $(a,a)$ được gọi là cạnh lặp (loop) và hai cạnh giữa cặp đỉnh $(b,d)$ được gọi là hai cạnh song song (parallel edges). Một đồ thị được gọi là một đơn đồ thị (simple graph) nếu nó không có cạnh lặp và cạnh song song (hình $(2)$). Nếu một đồ thị không phải là đơn đồ thị thì chúng ta sẽ goị nó là đa đồ thị (multigraph). Trong các loạt bài đồ thị ở đây, ta chủ yếu xét đơn đồ thị. Do đó, khi nói đồ thị ta sẽ ngầm hiểu là đơn đồ thị. Ta có:
Nếu đồ thị $G(V,E)$ vô hướng, với mỗi cạnh $uv$, đỉnh $v$ được gọi là kề (incident) với cạnh $uv$. Đỉnh $u$ được gọi là hàng xóm (neighbor) của $v$. Bậc (degree) của đỉnh $v$, thường kí hiệu là $d(v)$, là số hàng xóm của đỉnh $v$. Bổ đề sau đây cực kì quan trọng trong các thuật toán đồ thị:
$\sum_{u \in V}d(u) = 2m \qquad (1)$
Chứng minh: Mỗi đỉnh $u$ đặt một đồng trên cạnh kề với nó. Tổng số đồng xu đươcj các đỉnh đặt trên các cạnh là $\sum_{u \in V}d(u)$. Nhìn vào mỗi cạnh, ta sẽ thấy 2 đồng xu ở hai đầu mút. Do đó, tổng số đồng xu sẽ là $2m. \qquad \blacksquare$
Nếu đồ thị $G(V,E)$ có hướng, với mỗi cung $u\rightarrow v$, đỉnh $v$ được gọi là đỉnh liền sau (successor) của $u$ và đỉnh $u$ được gọi là đỉnh liền trước (predecessor) của $v$. Bậc liền trước (in-degree) của $v$ là số đỉnh liền trước $v$ và bậc liền sau (out-degree) của $v$ là số đỉnh liền sau $v$. Ví dụ bậc liền trước của $d$ trong hình $(3)$ là 1 và bậc liền sau là $3$.
Ta gọi $H(V_H, E_H)$ là đồ thị con (subgraph) của $G$ nếu $V_H \subseteq V$ và $E_H \subseteq E$.
Một đường đi (walk) là một dãy các cạnh ${e_1,e_2,\ldots, e_k}$ trong đó hai cạnh liền kề bất kì $e_i$ và $e_{i+1}$ đều có chung một đỉnh. Chú ý là đường đi có thể đi qua một đỉnh nhiều lần. Trong trường hợp mỗi đỉnh được thăm đúng 1 lần, ta sẽ gọi đó là đường đi đơn (path).
Ví dụ 1: trong đồ thì ở hình dưới đây, ${ab,bc,ca,ae,ed,dc}$ là một đường đi giữa $a$ và $c$ và ${ab,bd,dc}$ là một đường đi đơn giữa $a$ và $c$.
Một đường đi đóng (closed walk) là một đường đi bắt đầu và kết thúc tại cùng một điểm. Một chu trình (cycle) là một đường đi đơn bắt đầu và kết thúc tại cùng một điểm. (Chú ý chữ đơn trong định nghĩa của chu trình.) Có thể nói một chu trình là một đường đi đóng đi qua mỗi điểm đúng 1 lần ngoại trừ điểm đầu và điểm cuối. Các khái niệm vừa rồi nếu áp dụng cho đồ thị có hướng thì ta sẽ thêm từ “có hướng” vào đằng trước: đường đi có hướng, đường đi đơn có hướng, chu trình có hướng, vân vân.
Một đồ thị vô hướng được gọi là liên thông (connected) nếu tồn tại một đường đi giữa mọi cặp điểm. Một đồ thị có hướng gọi là liên thông (yếu) nếu đồ thị vô hướng thu được từ đồ thị đó bằng cách bỏ qua hướng của cạnh là liên thông. Một đồ thị có hướng gọi là liên thông mạnh (strongly connected) nếu tồn tại một đường đi có hướng giữa mọi cặp điểm. Hiển nhiên nếu một đồ thị có hướng liên thông mạnh thì nó cũng liên thông yếu. Tuy nhiên điều ngược lại chưa chắc đúng.
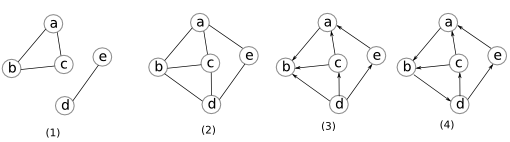
Ví dụ 2: Đồ thị $(1)$ dưới đây là không liên thông, đồ thị $(2)$ liên thông, đồ thị $(3)$ liên thông yếu (nhưng không mạnh) và đồ thị $(4)$ liên thông mạnh.
Nếu một đồ thị (vô hướng) không liên thông, tập các đỉnh liên thông với nhau tạo thành một thành phần liên thông (connected component). Tương tự như vậy ta có thể định nghĩa thành phần liên thông (yếu hay mạnh) cho đồ thị có hướng. Một đồ thị không có chu trình (acyclic) thì ta gọ là một rừng (forest). Một rừng chỉ có một thành phần liên thông thì ta gọi nó là một cây (tree). Khái niệm cây và rừng có hướng tương tự như đồ thị có hướng.
Có lẽ ta sẽ dừng định nghĩa khái niệm ở đây. Còn rất rất nhiều các khái niệm khác chúng ta sẽ định nghĩa khi mà chúng ta cần. Gần như tất cả các khái niệm cơ bản các bạn có thể tìm thấy ở tài liệu tham khoảo [2].
Trong phần tiếp theo, ta xét $G(V,E)$ vô hướng. Các thao tác với đồ thị có hướng có thể được mở rộng và áp dụng một cách tương tự.
Ghi chú 1: Các bạn không nhất thiết phải nhớ hết các khái niệm đã liệt kê ở đây, vì không phải bài nào chúng ta cũng sử dụng. Nhưng ta sẽ sử dụng hầu hết các khái niệm này trong các bài sau, do đó, lúc nào quên thì bạn đọc có thể xem lại mục này.
2. Biểu diễn đồ thị
Chúng ta có thể biểu diễn đồ thị bằng một ma trận kề (adjacency matrix) $A$ có kích thước $n \times n$ trong đó:
$A[u,v] = \begin{cases} 1, & \mbox{if } uv \in E\\ 0, & \mbox{otherwise } \end{cases} \qquad (2)$
Có thể thấy ngay là kích thước của cách biểu diễn này là $O(n^2)$ bất kể số lượng cạnh là nhiều hay ít. Theo tính chất 1, số lượng cạnh $m$ của một đồ thị có thể lên tới $O(n^2)$ cạnh (đồ thị dầy). Do đó, cách biểu diễn này có thể nói là phù hợp với đồ thị dầy. Tuy nhiên, nhiều đồ thị (đặc biệt các đồ thị thực tế như mạng xã hội), số lượng cạnh chỉ là $O(n)$ (đồ thị thưa). Do đó cách biểu diễn này khá tốn kém với đồ thị thưa.
Để tiết kiệm bộ nhớ, với mỗi đỉnh $u \in V$, ta lưu trữ một danh sách các đỉnh kề với nó. Như vậy, đỉnh $u$ cần một danh sách có $d(u)$ phần tử. Do đó tổng số phần tử của các danh sách là $2m$ theo bổ đề bắt tay. Cách biểu diễn như trên gọi là biểu diễn bằng danh sách kề (adjacency list). Cách biểu diễn này phù hợp với cả đồ thị thưa. Mặc dù tiết kiệm bộ nhớ, cách biểu diễn này không phù hợp với một số thao tác của đồ thị. Bảng dưới đây so sánh hai cách biểu diễn vừa trình bày.
| Adjacency matrix | Adjacency list (linked list) | |
| Space | $O(n^2)$ | $O(n+m)$ |
| Test $uv \in E$ | $O(1)$ | $O(1 + \min(d(u),d(v)))$ |
| List all neighbors of $v$ | $O(n)$ | $O(1+d(v))$ |
| Add an edge $uv$ | $O(1)$ | $O(1)$ |
| Delete an edge $uv$ | $O(1)$ | $O(d(u)+d(v)) = O(n)$ |
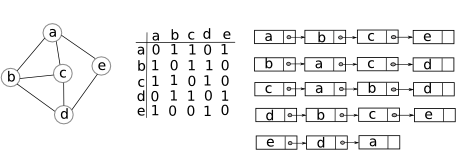
Ví dụ 3: Hình dưới đây minh hoạ hai cách biểu diễn đồ thị:
Ta còn có thể kết hợp cách biểu diễn danh sách kề với một vài cấu trúc dữ liệu khác. Cụ thể, thay vì dùng danh sách liên kết để biểu diễn các đỉnh kề với một đỉnh $u$, ta còn có thể dùng bảng băm hoặc cấu trúc cây để biểu diễn. Trong khuôn khổ các bài viết ở đây, ta ít dùng (hoặc không dùng) các cấu trúc như vậy.
Ngoài ra ta có thể biểu diễn đồ thị bằng cách liệt kê tất cả các cạnh $uv$ trong cùng một danh sách liên kế. Cách biểu diễn này, có tên là danh sách cạnh (edge list), có bộ nhớ $O(m)$. Tuy nhiên, việc thực hiện các thao tác cơ bản trong cách biểu diễn này sẽ rất tốn kém. Đôi khi, ta có thể kết hợp cách biểu diễn này với cách biểu diễn danh sách kề để tận dụng ưu thế của cả hai cách biểu diễn mà bộ nhớ vẫn là tuyến tính.
3. Duyệt đồ thị
Duyệt đồ thị là dạng bài toán, từ một đỉnh $v$, thăm tất cả các đỉnh $u$ khác có thể đi đến được (theo các cạnh) từ $v$. Ứng dụng phổ biến của duyệt đồ thị là tìm đường: tìm một đường đi trong đồ thị từ một đỉnh $s$ tới một đỉnh $t$, hay xác định các tính chất của đồ thị như: xác định xem đồ thị có liên thông (mạnh) hay không? đếm xem đồ thị có bao nhiêu thành phần liên thông mạnh?
Để đơn giản ta sẽ giả sử đồ thị là vô hướngg và liên thông. Nguyên lý duyệt đồ thị không liên thông và có hướng khá tương tự.
Để duyệt đồ thị ta thường bắt đầu từ một đỉnh $s$, sau đó thăm các hàng xóm của $s$, và từ các hàng xóm nay thăm tiếp các đỉnh khác. Cách thức thực thi như sau: Ta sẽ sử dụng 2 loại nhãn để gán cho các đỉnh của đồ thị: chưa thăm (unvisited) và đã thăm (visited). Ban đầu tất cả các đỉnh được đánh dấu là chưa thăm (unvisited). Ta sẽ duy trì một cấu trúc dữ liệu $C$, ban đầu chỉ chứa $s$. Ta sẽ thực hiện lặp 2 bước:
- Lấy ra một đỉnh $u$ trong $C$. Nếu $u$ có nhãn chưa thăm, ta sẽ cập nhật lại nhãn cho $u$ là đã thăm (visited).
- Đưa các hàng xóm của $u$ có nhãn chưa thăm vào trong $C$.
Thuật toán dừng khi $C = \emptyset$. Giả mã của thuật toán như sau:
1. mark all vertices unvisited
2. Add$(C,s)$
3. while $C \not= \emptyset$
4. $u \leftarrow$ Remove$(C)$
5. if $u$ is unvisited
6. mark $u$ visited
7. for all $uv \in E$ and $v$ is unvisited
8. Add$(C,v)$
Thủ tục Remove$(C)$ lấy ra một đỉnh trong $C$. Thủ tục Add$(C,v)$ đưa đỉnh $v$ vào trong tập $C$. Trước khi đi vào phân tích chi tiết, xét một số câu hỏi sau:
Câu hỏi 1: Tại sao ta phải kiểm tra ở dòng 5, trong khi mọi đỉnh được đưa vào $C$ trong dòng 7 đều có nhãn là unvisited?
Trả lời: Đó là vì có thể một đỉnh được đưa nhiều lần vào $C$, và lần đầu tiên nó được lấy ra khỏi $C$, nó được đánh dấu là visited, khi đó các bản khác trong $C$ đều có nhãn visited. Hay nói cách khác, tại một thời điểm bất kì trong quá trình chạy của thuật toán, $C$ có thể chưa đỉnh có nhãn visited. Cụ thể, xét đồ thị có 3 đỉnh $u,v,w$, đôi một kề nhau. Đỉnh $u$ được lấy ra từ $C$ đầu tiên; đánh dấu $u$ là đã thăm. Ngay sau đó, $v$ và $w$ sẽ được đưa vào $C$. Tiếp theo, lấy $v$ ra khỏi $C$ và đánh dấu $v$ là đã thăm. Lúc này ta lại tiếp tục đưa $w$ vào $C$ một lần nữa vì theo giả mã trên, $w$ là hàng xóm của $v$ và có nhãn chưa thăm.
Câu hỏi 2: Theo như câu trả lời ở trên, ta đã biết $C$ có thể chứa nhiều phiên bản của cùng một đỉnh. Tại sao ta không thực hiện kiểm tra xem một đỉnh có ở $C$ hay chưa trước khi đưa vào $C$?
Trả lời: Ta có thể làm như vậy, nhưng code sẽ phức tạp hơn một chút.
Câu hỏi 3: Một đỉnh bị đưa vào $C$ tối đa bao nhiêu lần?
Trả lời: Không quá $d(u)$ lần cho mỗi đỉnh $u$, do mỗi lần $u$ được đưa vào $C$, nó phải kề với một đỉnh được đánh dấu là đã thăm, và do đó đỉnh đó sẽ không được đưa lại vào $C$ nữa.
Từ các hỏi 3, ta thấy tập $C$ lưu các đỉnh kề với ít nhất một đỉnh đã thăm.
Phân tích thuật toán: Nếu đồ thị là liên thông, bằng quy nạp ta có thể chứng minh được mỗi đỉnh đều được đưa vào $C$ ít nhất một lần. Do đó, khi thuật toán kết thúc, mọi đỉnh có nhãn là đã thăm.
Để phân tích thời gia, ta giả sử rằng ta sử dụng một cấu trúc để thực thi $C$ sao cho việc thêm vào hoặc lấy một đỉnh bất kì (dòng 4 và dòng 8) được thực hiện trong thời gian $O(1)$ (ví dụ nếu thưc thi $C$ bằng danh sách liên kết thì thêm vào hoặc lấy ra đỉnh ở đầu danh sách có thể được thực hiện trong thời gian $O(1)$).
Không khó để thấy thời gian của thuật toán tỉ lệ với số lần ta thực hiện lệnh Add$(C,v)$ ở dòng 8. Theo như trả lời của câu hỏi 3, mỗi đỉnh được đưa vào $C$ với số lần tối đa là bậc của đỉnh đó. Do đó, tổng thời gian của thuật toán là $O(\sum_{v \in V} d(v)) = O(m)$, theo bồ đề bắt tay. $\blacksquare$
Trong trường hợp đồ thị không liên thông, ta phải duyệt qua từng thành phần liên thông một. Do đồ thị có tối đa $n$ thành phần liên thông, ta có:
Trong phân tích ở trên ta giả sử $C$ được thực thi sao cho việc lấy ra một phần tử (bất kì) và đưa vào một phần tử được thực hiện trong thời gian $O(1)$, do đó, danh sách liên kết là một cấu trúc phù hợp. Tuy nhiên, ta có thể sử dụng hàng đợi (Queue) hoặc ngăn xếp (Stack). Sử dụng hai cấu trúc này không chỉ đơn giản là hai cách thực thi khác, mà ta còn thu được các tính chất thú vị khác. Trường hợp ta thực thi $C$ bằng hàng đợi, ta gọi thuật toán là duyệt theo chiều rộng (Breath First Search - BFS). Trường hợp ta thực thi $C$ bằng ngăn xếp, ta gọi thuật toán là duyệt theo chiều sâu (Depth First Search - DFS). Sau đây ta sẽ thảo luận cả hai thuật toán.
4. Thuật toán duyệt theo chiều rộng
Như đã nói ở trên, thuật toán BFS sẽ thực thi $C$ bằng hàng đợi. Ta sẽ thay thủ tục Add$(C,v)$ bằng thủ tục Enqueue$(C,v)$ và thủ tục Remove$(C)$ bằng thủ tục Dequeue$(C)$. Ngoài khung cơ bản như thuật toán ở trên, ta sẽ gán cho mỗi đỉnh $v$ một nhãn $\ell[v]$. Giá trị của $\ell[v]$, như ta sẽ chỉ ra dưới đây, là khoảng cách ngắn nhất từ $s$ tới $v$. Giả mã như sau:
1. for each $v \in V$
2. $\ell[v] \leftarrow +\infty$
3. mark all vertices unvisited
4. $C\leftarrow$ an empty Queue
5. Enqueue$(C,s)$
6. $\ell[s] \leftarrow 0$
7. while $C \not= \emptyset$
8. $u \leftarrow$ Dequeue$(C)$
9. if $u$ is unvisited
10. mark $u$ visited
11. for all $uv \in E$ and $v$ is unvisited
12. Enqueue$(C,v)$
13. $\ell[v] \leftarrow \min(\ell[v],\ell[u]+1)$
Ghi chú 2: Hàng đợi là cấu trúc FIFO, ai vào trước thì ra trước. Ngoài ra, như phân tích ở thuật toán gốc, một đỉnh có thể bị đưa nhiều lần vào hàng đợi. Ta sẽ thấy trong phân tích dưới đây, chính điều này buộc ta phải sử dụng thao tác $\min$ ở dòng 13.
Hai dòng màu đỏ (dòng 6 và 13) là hai dòng khác biệt lớn nhất so với thuật toán gốc GenericGraphTraverse.
Ví dụ ta thực thi thuật toán trên với đồ thị trong hình bên trái và kết qủa thu được trong hình bên phải. Các số ứng với các đỉnh tương ứng là nhãn $\ell$ của các đỉnh đó. Những cạnh màu đỏ là những cạnh $uv$ mà $\ell[v]$ bị cập nhật lại thành $\ell[u] +1$ ở dòng 13.
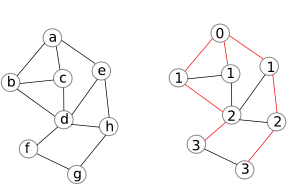
Chứng minh: Gọi mức (level) của một đỉnh $u$, kí hiệu là $level(u)$, là khoảng cách ngắn nhất từ đỉnh $s$ tới $u$. Trong ví dụ trên, các đỉnh ${b,c,e}$ đều có mức $1$, ${d,h}$ đề có mức 2, …. Ta có nhận xét sau:
Nhận xét: Các đỉnh ở mức $\geq i$ sẽ được đưa vào $C$ sau các đỉnh ở các mức $1,2,\ldots, i-1$.
Chú ý vì $C$ là một hàng đợi nên đỉnh nào được đưa vào trước sẽ được lấy ra trước. Do đó nhận xét trên cũng có nghĩa là các đỉnh có mức $< i$ sẽ được đánh dấu là visited trước các đỉnh mức $i$.
Ta chứng minh nhận xét trên bằng quy nạp. Trường hợp cơ sở là các đỉnh mức $0$ và chỉ có $s$ ở mức này. Giả sử nhận xét đúng với $i-1$, có nghĩa là các mức nhỏ hơn $i-1$ sẽ được đưa vào $C$ trước các đỉnh mức $ \geq i-1$.
Xét đỉnh $u$ ở mức $\geq i$. Ta phải chứng minh $u$ được đưa vào sau các đỉnh mức $i-1$. Gọi $v$ là một đỉnh mức $i-1$, nó phải có một hàng xóm $w$ có mức $i-2$ và không mất tính tổng quát, giả sử $w$ là hàng xóm có mức $i-2$ được đưa vào $C$ đầu tiên trong số các hàng xóm có mức $i-2$ của $v$. Theo định nghĩa của mức, $d(u,s) = i$, do đó, mọi hàng xóm của nó đều có mức $\geq i-1$. Theo giả thiết quy nạp, mọi hàng xóm của $u$ đều bị đưa vào sau $w$. Theo tính FIFO của hàng đợi, $w$ được lấy ra trước hàng xóm của $u$, và do đó, $v$ sẽ được đưa vào trước $u$ khi ta duyệt các hàng xóm của $w$ trong dòng 11 và 12. Như vậy, nhận xét là đúng.
Phần còn lại của chứng minh, ta quy nạp trên biến $level$ để chứng minh rằng nhãn của $v$ cũng chính là mức của $v$, i.e, $level(v) = \ell[v]$.
Xét một đỉnh $v$. Lần đầu tiên $v$ được đưa vào hàng đợi $C$ là khi ta thăm một đỉnh $u$ nào đó kề với $v$ và theo nhận xét trên, mức của $u$ sẽ nhỏ hơn mức của $v$. Từ định nghĩa của mức ta suy ra $level(u) = level(v)-1$. Theo giả thiết quy nạp $\ell[u] = level(u)$, ta suy ra $level(v) = \ell[u] +1$. Theo giả mã, khi đưa $v$ vào hàng đợi, ta cập nhật $\ell[v] = \min(+\infty,\ell[u]+1) = \ell[u]+1$. Do đó, $\ell[v] = lelve(v)$. $\blacksquare$
Kết hợp Định lý 1 và Định lý 2 ta có hệ quả sau:
Hệ quả có ý nghĩa rất lớn vì sau này ta sẽ tìm hiểu, thuật toán tốt nhất tìm đường đi ngắn nhất với đồ thị có trong số có thời gian $O(n\log n)$ ngay cả trong đồ thị thưa $m = O(n)$. Thuật toán BFS sẽ là thuật toán đơn giản và hiệu quả để tìm đường đi ngắn nhất trong đồ thị không có trong số.
5. Thuật toán duyệt theo chiều sâu
Trong duyệt theo chiều sâu (DFS), ta thực thi $C$ sử dụng ngăn xếp. Ta sẽ thay thủ tục Add$(C,v)$ bằng thủ tục Push$(C,v)$ và thủ tục Remove$(C)$ bằng thủ tục Pop$(C)$.
$C\leftarrow$ an empty Stack
Push$(C,s)$
while $C \not= \emptyset$
$u \leftarrow$ Pop$(C)$
if $u$ is unvisited
mark $u$ visited
for all $uv \in E$ and $v$ is unvisited
Push$(C,v)$
Nếu chỉ nhìn qua thi không thấy sự khác biệt quá nhiều giữa DFS và thuật toán chung để duyệt đồ thị. Tuy nhiên bằng cách cập nhật thêm một vài thông tin trong quá trình duyệt đồ thị (giống như BFS), ta có thể phát hiện ra những tính chất rất thú vị của DFS. Trong bài này, ta tạm thời chưa đi sâu vào các ứng dụng đó. Trong bài tập 6, ta sẽ tham khảo một ứng dụng của DFS. Hình dưới đây là một ví dụ thực thi DFS trên đồ thị. Số tương ứng của mỗi đỉnh ở bên phải là thứ tự của đỉnh thăm bởi DFS.
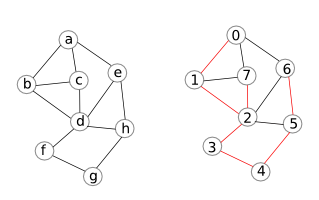
Ngoài thủ tục lặp DFS sử dụng ngăn xếp như trên, ta còn có thể thực thi DFS sử dụng đệ quy:
mark $s$ visited
for all $sv \in E$ and $v$ is unvisited.
RecursiveDFS($v$)
Ta thấy cách thứ hai đơn giản hơn do không phải thực thi Stack. Tuy nhiên, cách này sẽ sử dụng nhiều Call Stack của máy tính và trong trường hợp độ sâu đệ quy lớn có thể gây ra Stack Overflow.
6. Tham khảo
[1] Jeff Erickson, Graph Lecture Note, UIUC.
[2] Diestel, Reinhard. Graph theory. 2005. Grad. Texts in Math (2005).
[3] Cormen, Thomas H.; Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford. Introduction to Algorithms (2nd ed.), Chapter 23. MIT Press and McGraw-Hill (2001). ISBN 0-262-03293-7.
7. Bài tập
Bài 1: Một cây (vô hướng) được gọi là nhị phân nếu nó chỉ có một đỉnh đặc biệt (gọi là gốc) có bậc 2, còn các đỉnh khác hoặc có bậc 3, hoặc có bậc 1. Các đỉnh bậc 1 được gọi là lá của cây. Gọi $L$ là số nút lá của một cây nhị phân $n$ nút. Chứng minh rằng $n = 2L-1$.
Bài 2: Thực thi các cách duyệt đồ thị BFS và DFS bằng ngôn ngữ C.
Bài 3: Cho một đồ thị vô hướng $G(V,E)$, thiết kế thuật toán đếm số thành phần liên thông của đồ thị trong thời gian $O(n+m)$.
Bài 4: Cho một đồ thị vô hướng, liên thông $G(V,E)$, và hai đỉnh $s,t$. Tìm một đường đi từ $s$ tới $t$ trong thời gian $O(m+n)$.
Bài 5: Một đồ thị vô hướng được gọi là hai phía (bipartite) nếu như tập đỉnh $V$ có thể được phân thành hai tập rời nhau $A,B$ sao cho $V = A\cup B$ và các cạnh của đồ thị chỉ nối một đỉnh thuộc $A$ và một đỉnh thuộc $B$. Nói các khác, không có cạnh nào giữa hai đỉnh cùng thuộc $A$ hoặc cùng thuộc $B$. Sử dụng BFS, thiết kế thuật toán xác định xem một đồ thị vô hướng $G(V,E)$ cho trước có phải là đồ thị hai phía hay không. Có thể giả sử đồ thị liên thông, và thuật toán phải chạy trong thời gian $O(n+m)$.
Bài 6: Cho một đồ thị có hướng $G(V,E)$, sử dụng DFS xác định xem đồ thị có một chu trình có hướng hay không trong thời gian $O(n+m)$.
Gợi ý: chọn một đỉnh $s$ bất kì, và thăm DFS tại $s$. Quá trình thăm DFS tại một đỉnh $s$ bất kì sẽ cho ta một cây DFS, gốc tại $s$ và các cung hướng ra ngoài $s$. (Cây này có thể không phủ toàn bộ đỉnh vì có thể có đỉnh không có đường đi có hướng từ $s$ tới nó.) Ta gọi một nút $v$ là con cháu của nút khác $u$ trong cây DFS nếu có đường đi (có hướng) từ $u$ đến $v$ trong cây. Ta sẽ dùng thêm nhãn visiting, ngoài hai nhãn univisited và visited. Ta sẽ đánh dấu một đỉnh là visiting khi ta bắt đầu thăm nó, và ta chỉ đổi nhãn của nó sang visited, nếu tất cả đỉnh con cháu của nó đều có nhãn visited. (Một nút là lá của cây DFS thì sẽ bị đánh dấu visited ngay sau khi nó được đánh dấu visiting.) Điều gì sẽ xảy ra nếu trong quá trình thăm, ta thấy một cung $u\rightarrow v$ trong đó $v$ có nhãn visiting?