Quay Lui
Bài 4: Quay lui
Quy lui là một kĩ thuật thiết kế giải thuật dựa trên đệ quy. Ý tưởng của quay lui khá đơn giản:
Nguyên lý: Tìm lời giải từng bước, mỗi bước chọn một trong số các lựa chọn có thể (dẫn đến lời giải) và đệ quy.
Vấn đề khó nhất khi thiết kế thuật toán dạng quay lui đó là tìm ra tập các lựa chọn có thể trong mỗi bước. Tập lựa chọn này sẽ ảnh hưởng đến tính chính xác cũng như độ phức tạp (thời gian cũng như bộ nhớ) của thuật toán quay lui. Để minh hoạ, ta xét một vài ví dụ về thiết kế thuật toán theo kĩ thuật quay lui.
1. Bài toán $n$ quân hậu
Bài toán này khá cổ điển và được phát biểu như sau:
Ta sẽ áp dụng thuật toán quay lui để giải bài toán này. Trong phần nguyên lý, ta đã nói là sẽ tìm lời giải theo từng bước. Do đó, vấn đề đầu tiên đặt ra đó là ta phải ghi nhớ (hay mã hoá) các lựa chọn mà ta đã thực hiện trước đó.
Mã hóa lựa chọn: Vị trí của mỗi quân hậu sẽ xác định bởi hàng và cột của bàn cờ. Ta có thể lựa chọn mã hoá một quân hậu bằng một mảng kiểu boolean $M$ trong đó $M[i,j] = $True nếu có một quân hậu ở hàng $i$ và cột $j$ và $M[i,j] = $False nếu ngược lại. Cách mã hoá này tuy đúng nhưng chưa hay, vì nó cần đến $O(n^2)$ bộ nhớ trong khi chỉ có $n$ quân hậu. Cách mã hoá ta sử dụng trong bài này là như sau:
Cách mã hoá này còn có 2 lợi ích sau: (a) Không có hai quân hậu nào cùng một hàng vì với mỗi hàng $i$, chỉ có đúng một giá trị $Q[i]$ và (b) để kiểm tra hai quân hậu $i \not= j $ có cùng cột hay không, ta chỉ việc kiểm tra $Q[i]$ và $Q[j]$ có khác nhau hay không.
Với cách mã hoá mảng boolean như ở trên, kiểm tra cùng hàng hay cùng cột khá bất tiện: ta phải duyệt qua ma trận $M$.
Câu hỏi cho bạn đọc: giả sử ta dùng mảng vị trí $Q$ để mã hoá như trên, làm thế nào để kiểm tra xem hai quân hậu có cùng đường chéo hay không?
Ghi chú 1: trả lời được câu hỏi này chính là giải được toàn bộ bài toán. Trước khi đọc tiếp, bạn nên dành thời gian (ít nhất khoảng 10 phút) để suy nghĩ về câu hỏi trên.
Trả lời: Hai quân hậu đặt ở hai vị trí $(i,j)$ và $(a,b)$ ăn được nhau theo đường chéo khi và chỉ khi $i-j = a-b$ hoặc $i+j = a+b$.
Ý tưởng chính của thuật toán quay lui: giả sử chúng ta đã đặt được $r-1$ quân hậu, $1 \leq r < n$, trên $r-1$ hàng đầu tiên sao cho không có 2 quân hậu nào ăn được nhau. Cụ thể các phần tử $Q[1,2,\ldots, r-1]$ sẽ khác $0$ và các phần tử $Q[r,r+1. \ldots, n]$ đều bằng $0$. Chúng ta tìm cách đặt một quân hậu trên hàng thứ $r$. Ta sẽ thử lần lượt đặt vào cột thứ $1,2,\ldots, n$. Nếu đặt vào cột thứ $j$ mà bị một trong $r$ quân hậu đã đặt trước đó ăn, ta sẽ thử cột thứ $j+1$. Nếu ta tìm được một ví trí đặt khả dĩ, ta sẽ đặt vào đó và gọi đệ quy để đặt hàng thứ $r+1$. Giả mã như sau:
1. if$(r = n+ 1)$
2. print $Q$ and exit
3. else
4. for $j \leftarrow 1$ to $n$
5. $legal \leftarrow $ True
6. for $i \leftarrow 1$ to $r-1$ $\ll$ check conflict $\gg$
7. if $(Q[i] = j)$ or $(Q[i] = j+r-i)$ or $(Q[i] = j-r+i)$
8. $legal \leftarrow $ False
9. if $legal =$ True
10. $Q[r] \leftarrow j$
11. RecursiveQueen($Q[1,2,\ldots, n],r+1$)
Để tìm một cách đặt quân hậu trên $n$ bàn cờ, ta chỉ việc gọi:
$Q[1,\ldots, n]\leftarrow [0,\ldots, 0]$
RecursiveQueen($Q[1,2,\ldots, n],1$)
Tính đúng đắn của thuật toán: Ta chứng minh rằng khi thuật toán kết thúc (dòng số 2, khi ta in $Q$ và thoát khỏi chương trình), thì $Q$ mã hoá một cách đặt $n$ quân hậu trên bàng cờ một cách hợp lệ. Do đây là thuật toán đệ quy, ta thường sử dụng kĩ thuật quy nạp để chứng minh.
Ta sẽ chứng minh bằng quy nạp rằng: mỗi khi đặt một quân hậu mới vào hàng thứ $r$ thì không có hai quân hậu nào ăn được nhau trong số các quân hậu đã được đặt từ hàng $1$ đến $r$. Khi $r=1$, điều này hiển nhiên đúng vì ta chỉ có 1 quân hậu. Theo giả thiết quy nạp, ta có thể giả sử không có hai quân hậu nào ăn được nhau trong số các quân hậu đã được đặt từ hàng $1$ đến $r-1$. Do đó, ta chỉ cần chứng minh quân hậu ở hàng thứ $r$ không thể ăn được các quân hậu đã đặt trong các hàng trước đó. Điều này rõ ràng là đúng vì trước khi đặt quân hậu thứ $r$ vào cột thứ $j$, ta đã kiểm tra tính chất này (dòng số 7), và nếu quân hậu $r$ có thể ăn được bất kì quân hậu nào trước đó, thuật toán sẽ thiết lập $legal = $False, và do đó, dòng thứ 10 sẽ không được thực thi (có nghĩa là quân hậu đó sẽ không được đặt vào cột $j$). Đây chính là dpcm.
Phân tích thời gian: Gọi $T(i)$ là thời gian để đặt $i$ quân hậu còn lại lên bàn cờ. Ta nói còn lại vì ta giả sử trước đó ta đã đặt $n-i$ quân hậu lên bàn cờ. Theo định nghĩa này, thời gian của thuật toán là $T(n)$ vì ban đầu ta “còn lại” $n$ quân hậu. Dễ thấy trong dòng 4, ta lặp $n$ lần. Mỗi lần lặp thuật toán sẽ có thể sẽ đặt được một quân hậu mới và gọi đệ quy để đặt $i-1$ quân hậu còn lại. Thời gian để tìm vị trí hợp lệ cho quân hậu mới (dòng 6-7-8) là $O(n)$. Do đó, ta có:
Giải phương trình trên ta được $T(n) = O(n^n)$.
Ghi chú 2: Phân tích một cách chặt chẽ hơn, dễ thấy khi đặt quân hậu mới (thứ $n-i+1$) thì $n-i$ quân hậu đã được đặt vào $n-i$ cột. Do đó, dòng 4 của thuật toán sẽ không gọi đệ quy với ít nhất $n-i$ giá trị của $j$. Do đó ta có:
Giải ra ta sẽ được $T(n) = O((n!) n)$. Con số này nhỏ hơn $O(n^n)$ một chút.
Cây đệ quy là một cách nhìn khác của thuật toán. Tưởng tượng ta có một cây với gốc tượng trưng cho cấu hình ban đầu của bàn cờ (mảng $Q[1,2,\ldots,n]$ gồm toàn 0). Nút con của gốc, gọi là nút mức 1, là các cách đặt một quân hậu vào hàng thứ 1. Nút con của một nút mức 1, gọi là nút mức 2, là các cách đặt khả dĩ một quân hậu vào hàng thứ 2. Cứ như thế đến nút mức $n$ ta sẽ thu được một cây gọi là cây đệu quy. Có thể thấy rằng thuật toán quay lui ở trên thực ra chính là một cách duyệt cây (theo chiều sâu) cho đến khi tìm được một nút ở mức $n$. Hình minh họa sau với $n=4$ được lấy từ [1]
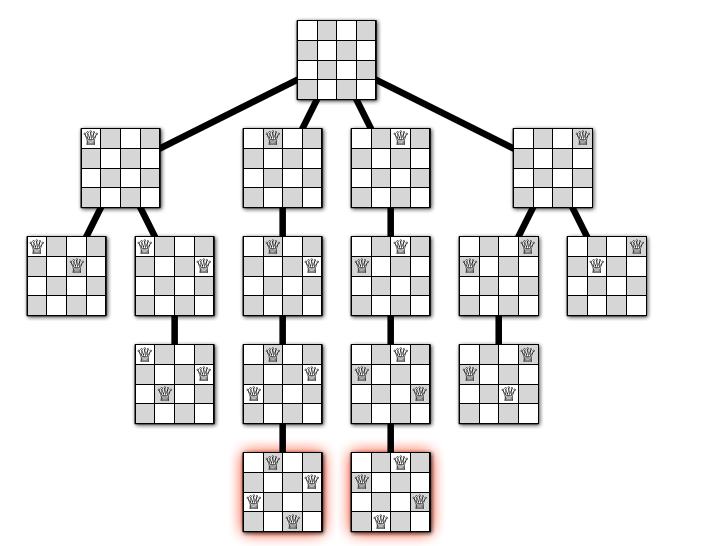
Nếu phân tích kĩ, ta sẽ thấy cây này chỉ có $O(n!)$ nút. Ở mỗi nút của cây, ta dành thờ gian $O(n)$ để kiểm tra tính hợp lệ của một cách đặt (dòng 6-7-8). Do đó tổng thời gian là $O((n!) n)$.
Ghi chú 3: Tồn tại một công thức dạng đóng để giải bài toán quân hậu với thời gian ($O(n)$) (để in ra lời giải) [3].
2. Sudoku
Sudoku là một trò chơi khá phổ biến và chắc ai cũng biết. Trò chơi như sau: có một hình vuông được chia thành 9x9 ô vuông con. Mỗi ô vuông con có giá trị trong khoảng từ 1 đến 9. Ban đầu hình vuông có một số ô vuông con cho trước (có điền sẵn số) và còn lại là trống. Hãy điền các số từ 1-9 vào các ô con lại sao cho: hàng ngang là các số khác nhau từ 1 đến 9, hàng dọc là các số khác nhau từ 1 đến 9, và mỗi khối 3x3 chính là các số khác nhau từ 1 đến 9. Ví dụ một câu đố và lời gải tương ứng như sau (hình được lấy từ wikipedia):
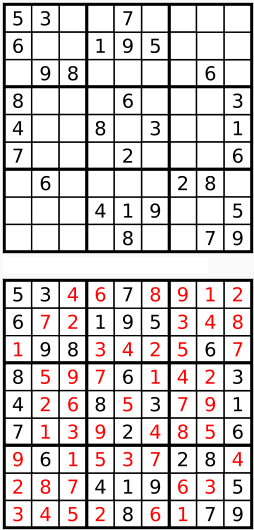
Quay lui thường là phương pháp chuẩn để giải các bài toán dạng sudoku. Ý tưởng của thuật toán cũng giống bài toán $n$ quân hậu. Mỗi bước tìm tập các giá trị khả dĩ để điền vào ô trống, và sau đó đệ quy để điền ô tiếp theo. Ở đây ta không cần phải nghĩ nhiều đến cách làm sao để mã hoá lời giả: chỉ đơn giản dùng một mảng $9\times 9$ $S$ và thiết lập $S[i,j] = k$ nếu ta muốn điền số $k$ vào ô $(i,j)$. Giả mã của thuật toán như sau:
if $y = 10$
if $x = 9$
print $S$
else
Sudoku($S[1,2,\ldots, 9][1,2,\ldots, 9],x+1,1$)
else if $S[x,y] = \emptyset$
for $k \leftarrow 1$ to $9$
if Feasible$(S,x,y,k)$
$S[x,y] \leftarrow k$
Sudoku($S[1,2,\ldots, 9][1,2,\ldots, 9],x,y+1$)
$S[x,y] \leftarrow \emptyset$ $\ll$ for next branching $\gg$
else $\ll S[x,y]$ is given $\gg$
Sudoku($S[1,2,\ldots, 9][1,2,\ldots, 9],x,y+1$)
Ý nghĩa của thủ tục Sudoku($S[1,2,\ldots, 9][1,2,\ldots, 9],x,y$) đó là “tìm giá trị cho ô $(x,y)$ của mảng $S$”. Thủ tục Feasible$(S,x,y,k)$ kiểm trả xem giá trị $k$ có hợp lệ với ô $S[x][y]$ không: giá trị này là hợp lệ nếu nó không vi phạm luật chơi (đã mô tả ở trên). Giả mã của thủ tục Feasible$(S,x,y,k)$ như sau:
for $i \leftarrow 1$ to $9$
if $S[x,i]=k$
return False
for $i \leftarrow 1$ to $9$
if $S[i,y]=k$
return False
$a \leftarrow \lfloor (x-1)/3 \rfloor, b \leftarrow \lfloor (y-1)/3 \rfloor $
for $i \leftarrow 3a+1$ to $3a+3$
for $j \leftarrow 3b+1$ to $3b+3$
if $S[i,j] = k$
return False
return True
Do đầu vào chỉ là $9x9$, hiển nhiên thời gian là $O(1)$. Chứng minh tính đúng đắn của thuật toán không quá khó; sử dụng quy nạp. Chi tiết coi như bài tập.
3. Subset Sum
Bài toán Subset Sum được phát biểu như sau:
Ví dụ: $X = {8,6,7,5,3,10,9}$ và $T = 12$. Lời giải là có tồn tại vì tập con ${7,5}$ của $X$ có tổng bằng 12.
Ta sẽ thiết kế thuật toán quay lui để giải bài toán Subset Sum. Ý tưởng của thuật toán dựa trên nhận xét sau: xét một phần tử $x \in X$, tồn tại một dãy con có tổng bằng $T$ nếu một trong hai điều kiện sau là đúng:
- Tồn tại một tập con của $X \setminus \{x\}$ có tổng bằng $T - x$
- Tồn tại một tập con của $X \setminus \{x\}$ có tổng bằng $T$
Giả mã của thuật toán:
if $T = 0$
return True
else if $T$ > $0$ and $n = 0$
return False
return SubsetSum$(X[1,2,\ldots,n-1],T)$ Or
SubsetSum$(X[1,2,\ldots,n-1],T- X[n])$
Tính đúng đắn của thuật toán coi như bài tập cho bạn đọc (bài tập 2 dưới đây).
Phân tích thời gian: Ở mỗi bước của thuật toán quay lui, ta gọi đệ quy hai lần trên mảng con của $X$ với kích thước nhỏ hơn 1. Ta có:
$ T(n) = 2T(n-1) + O(1) \qquad (3)$
Giả phương trình (3) ta được $T(n) = O(2^n)$.
4. Tài liệu tham khảo
[1] J. Erickson. Algorithm Lecture Notes, UIUC.
[2] $n$ queen on stackexchange: http://cstheory.stackexchange.com/questions/12682/is-the-n-queens-problem-np-hard
[3] B. Bernhardsson, Explicit Solutions to the N-queens Problem for All N, SIGART Bull. 2(2)(1991)7.
5. Bài tập
Bài 1: Chứng minh tính đúng đắn của thuật toán đệ quy cho bài toán Sodoku bằng quy nạp.
Bài 2: Chứng minh tính đúng đắn của thuật toán đệ quy cho bài toán Subset sum bằng quy nạp.
Bài 3: Hãy sửa đổi thuật toán quay lui ở trên của bài toán Subset Sum để in ra ít nhất một dãy con có tổng bằng $T$ của $X$.
Bài 4: Thực thi giả mã của các thủ tục đệ quy trong bài viết bằng ngôn ngữ $C$. Vẽ đồ thị thời gian của thuật toán cho bài toán $n$ quân hậu khi $n = 4,5,6,7,8$. Liệu code của bạn có thể chạy được trong thời gian $1$ s khi $n = 20$ không?
Bài 5: (Longest Increasing Subsequence) Cho một mảng $n$ phần tử $A[1,2,\ldots,n]$. Tìm một dãy dài nhất ($k$ lớn nhất) các chỉ số $1 \leq i_1$ < $i_2 $<$ \ldots $<$ i_k \leq n $ sao cho $A[i_1] \leq A[i_2] \leq \ldots \leq A[i_k]$ bằng phương pháp quay lui.
Gợi ý: xét $A[1]$, nếu $A[1]$ nằm trong dãy con tăng, đệ quy trên $A[2,3,\ldots]$ tìm dãy con tăng dài nhất mà mọi phần tử đều lớn hơn $A[1]$. Nếu $A[1]$ không nằm trong dãy con tăng, đệ quy trên $A[2,3,\ldots,n]$.
Bài 6: (Dãy gia tốc) Một dãy $X[1,2,\ldots,n]$ gọi là gia tốc nếu $2X[i]$ > $ X[i-1] + X[i+1]$. Cho một dãy $A[1,2,\ldots,n]$, tìm dãy con gia tốc dài nhất của $A$. Tìm công thức đệ quy cho bài toán, dựa vào đó thiết kế giải thuật quay lui.